已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为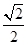 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
.
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足 +
+ =t
=t (O为坐标原点),当|
(O为坐标原点),当|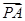 -
- |<
|< 时,求实数t的取值范围.
时,求实数t的取值范围.
.(本小题满分14分)
已知数列 的相邻两项
的相邻两项 是关于
是关于 的方程
的方程 的两实根,且
的两实根,且 ,记数列
,记数列 的前
的前 项和为
项和为 .
.
(1)求 ;
;
(2)求证:数列 是等比数列;
是等比数列;
(3) 设
设 ,问是否存在常数
,问是否存在常数 ,使得
,使得 对
对 都成立,若存在,
都成立,若存在,
求出 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
(本小题满分14分)
如图,椭圆
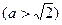 的离心率为
的离心率为 ,其两焦点分别为
,其两焦点分别为 ,
, 是椭圆在第一象限弧上一点,并满足
是椭圆在第一象限弧上一点,并满足 ,过
,过 作倾斜角互补的两条直线
作倾斜角互补的两条直线
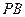 分别交椭圆于
分别交椭圆于
 两点.
两点.
(1)求椭圆
 的方程.
的方程.
(2)求 点坐标;
点坐标;
(3)当直线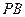 的斜率为
的斜率为 时,求直线
时,求直线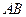 的方程.
的方程.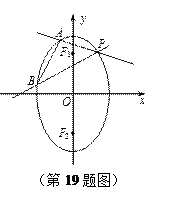
(本小题满分14分)
已知直角梯形 中(如图1),
中(如图1),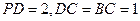 ,
,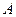 为
为 的中点,
的中点,
将 沿
沿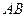 折起,使面
折起,使面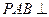 面
面 (如图2),点
(如图2),点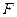 在线段
在线段 上,
上,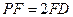 .
.
(1)求异面直线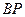 与
与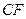 所成角的余弦值;
所成角的余弦值;
(2)求二面角 的余弦值;
的余弦值; (3)在四棱锥
(3)在四棱锥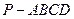 的棱
的棱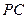 上是否存在一点
上是否存在一点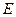 ,使得
,使得 平面
平面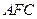 ,若存在,求出
,若存在,求出 点的位置,若不存在,请说明理由.
点的位置,若不存在,请说明理由.
(本小题共14分)
某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、
B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如下表: 如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
(本小题满分12分)
在 中,角
中,角 所对的边长分别为
所对的边长分别为 ,
, ,
,  ,
, 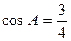 ,(1)求
,(1)求 的值;(2)求
的值;(2)求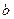 的值.
的值.