已知定点A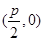
(p为常数，p>0)，B为x轴负半轴上的一个动点，动点M使得|AM|＝|AB|，且线段BM的中点G在y轴上．
(1)求动点M的轨迹C的方程；
(2)设EF为曲线C的一条动弦(EF不垂直于x轴)，其垂直平分线与x轴交于点T(4,0)，当p＝2时，求|EF|的最大值．
已知函数f(x)＝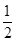
x2－mlnx＋(m－1)x，当m≤0时，试讨论函数f(x)的单调性；
已知函数f(x)＝x3－ax－1.
(1)若a＝3时，求f(x)的单调区间；
(2)若f(x)在实数集R上单调递增，求实数a的取值范围；
(3)是否存在实数a，使f(x)在(－1，1)上单调递减？若存在，求出a的取值范围；若不存在，说明理由．
已知函数f(x)＝lnx，g(x)＝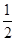
ax2＋bx(a≠0)，设函数f(x)的图象C1与函数g(x)的图象C2交于两点P、Q，过线段PQ的中点R作x轴垂线分别交C1、C2于点M、N，问是否存在点R，使C1在点M处的切线与C2在点N处的切线互相平行？若存在，求出点R的横坐标；若不存在，请说明理由．
求抛物线y＝x2上点到直线x－y－2＝0的最短距离．
已知曲线y＝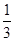
x3＋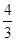
，求曲线过点P(2，4)的切线方程；