已知椭圆C: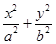 =1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+
=1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+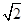 =0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.
=0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.
(1)求椭圆C的方程;
(2)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=4,证明:直线AB过定点 .
.
如图是三棱柱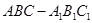 的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,
的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形, 为
为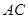 的中点.
的中点.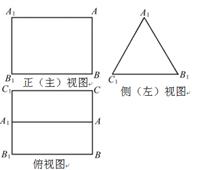
(1)求证: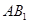 ∥平面
∥平面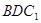 ;
;
(2)设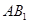 垂直于
垂直于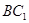 ,且
,且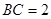 ,求点
,求点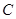 到平面
到平面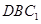 的距离.
的距离.
已知正方形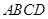 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点.
(1)在正方形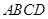 内部随机取一点
内部随机取一点 ,求满足
,求满足 的概率;
的概率;
(2)从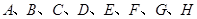 这八个点中,随机选取两个点,记这两个点之间的距离的平方为
这八个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求
,求 .
.
已知函数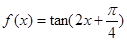 .
.
(1)求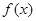 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)设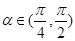 ,若
,若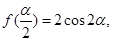 求
求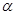 的大小.
的大小.
已知公差大于零的等差数列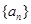 的前n项和为
的前n项和为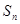 ,且满足:
,且满足: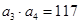 ,
,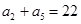 .
.
(1)求数列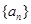 的通项公式
的通项公式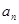 ;
;
(2)若数列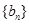 是等差数列,且
是等差数列,且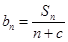 ,求非零常数c;
,求非零常数c;
(3)在(2)的条件下,设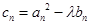 ,已知数列
,已知数列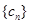 为递增数列,求实数
为递增数列,求实数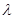 的取值范围.
的取值范围.
在数列{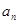 }中,
}中,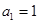 ,
, ,设
,设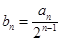 ,
,
(1)证明:数列{ }是等差数列;
}是等差数列;
(2)求数列{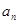 }的前n项和
}的前n项和 ;
;
(3)设 ,证明:
,证明: