如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=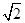 .
.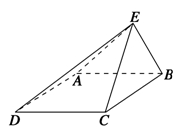
(1)求证:平面EAB⊥平面ABCD;
(2)求直线AE与平面CDE所成角的正弦值.
(本小题满分12分)已知函数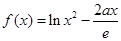 ,(
,(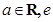 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求函数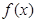 的递增区间;
的递增区间;
(Ⅱ)当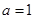 时,过点
时,过点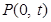
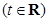 作曲线
作曲线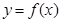 的两条切线,设两切点为
的两条切线,设两切点为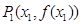 ,
,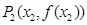
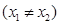 ,求证
,求证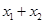 为定值,并求出该定值。
为定值,并求出该定值。
(本小题满分12分)已知椭圆的中心在原点,焦点在 轴上,离心率为
轴上,离心率为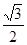 ,且经过点
,且经过点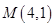 ,直线
,直线 交椭圆于不同的两点A,B.(Ⅰ)求椭圆的方程;
交椭圆于不同的两点A,B.(Ⅰ)求椭圆的方程;
(Ⅱ)求 的取值范围;(Ⅲ)若直线
的取值范围;(Ⅲ)若直线 不过点M,试问
不过点M,试问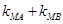 是否为定值?并说明理由。
是否为定值?并说明理由。
(本小题满分12分)
对某校高三年级学生参加社区服务次数进行统计, 随机抽取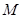 名学生作为样本,得到这
名学生作为样本,得到这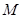 名学生参加社区服务的次数.
名学生参加社区服务的次数.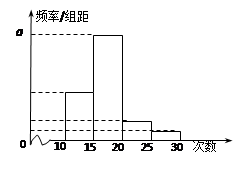
根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 |
频数 |
频率 |
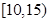 |
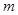 |
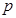 |
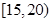 |
24 |
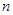 |
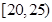 |
4 |
0.1 |
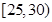 |
2 |
0.05[ |
| 合计 |
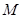 |
1 |
(Ⅰ)求出表中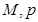 及图中
及图中 的值;
的值;
(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间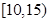 内的人数;
内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间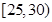 内的概率.
内的概率.
(本小题满分12分)如图,在四棱锥P-ABCD的底面是边长为2的正方形,
PD⊥平面ABCD,E、F分别是PB、AD的中点,PD=2.
(1)求证:BC⊥PC;
(2)求证:EF//平面PDC;
(3)求三棱锥B—AEF的体积。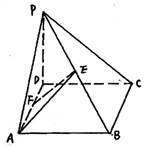
(本小题满分12分)
已知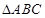 中,
中,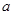 、
、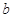 、
、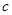 是三个内角
是三个内角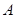 、
、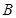 、
、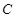 的对边,关于
的对边,关于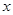 的不等式
的不等式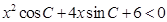 的解集是空集.
的解集是空集.
(1)求角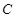 的最大值;
的最大值;
|
(2)若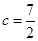 ,
,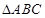 的面积
的面积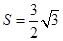 ,求当角
,求当角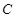 取最大值时
取最大值时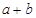 的值.
的值.