一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(1)求取出的3个球编号都不相同的概率;
(2)记X为取出的3个球中编号的最小值,求X的分布列与数学期望.
已知数列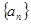 的前
的前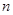 项的和为
项的和为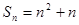 ,
, 是等比数列,且
是等比数列,且 ,
,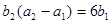 。
。
⑴求数列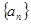 和
和 的通项公式;
的通项公式;
⑵设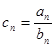 ,求数列
,求数列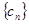 的前
的前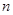 项的和
项的和 。
。
⑵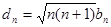 ,数列
,数列 的前
的前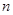 项的和为
项的和为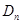 ,求证:
,求证: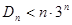 .
.
甲船由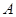 岛出发向北偏东
岛出发向北偏东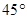 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为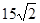 海里∕小时,在甲船从
海里∕小时,在甲船从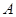 岛出发的同时,乙船从
岛出发的同时,乙船从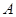 岛正南
岛正南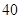 海里处的
海里处的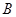 岛出发,朝北偏东
岛出发,朝北偏东 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为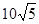 海里∕小时。
海里∕小时。
⑴求出发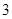 小时时两船相距多少海里?
小时时两船相距多少海里?
⑴两船出发后多长时间相距最近?最近距离为多少海里?
解关于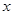 的不等式
的不等式
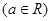
某村计划建造一个室内面积为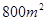 的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留
的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留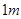 宽的通道,沿前侧内墙保留
宽的通道,沿前侧内墙保留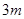 宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
已知数列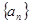 是公差不为零的等差数列,
是公差不为零的等差数列,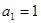 ,且
,且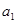 、
、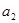 、
、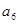 成等比数列。
成等比数列。
⑴求数列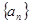 的通项公式;
的通项公式;
⑵设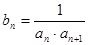 ,求数列
,求数列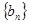 的前
的前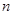 项和
项和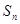 。
。