2x2-3x-5=0
如图①,直线AB的解析式为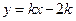 (
( )与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A
)与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A
求C点的坐标;
如图②,过
 作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
在⑵的条件下,连接
 与⊙
与⊙ 交于点G,点P为劣弧G F上一个动点,连接GP与EF的延长线交于H点,连接EP与OG交于I点,当P在劣弧G F运动时(不与G、F两点重合),
交于点G,点P为劣弧G F上一个动点,连接GP与EF的延长线交于H点,连接EP与OG交于I点,当P在劣弧G F运动时(不与G、F两点重合), 的值是否发生变化,若不变,求其值,若发生变化,求出其值的变化范围.
的值是否发生变化,若不变,求其值,若发生变化,求出其值的变化范围.
如图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0)
试写出点A,B之间的距离d(厘米)
与时间t(秒)之间的函数表达式;问点A出发后多少秒两圆相切?
我县华联超市服装柜台在销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元,为了迎接“元旦”佳节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件,要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少?
已知关于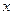 的一元二次方程
的一元二次方程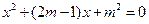 有两个实数根
有两个实数根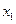 和
和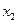 .
.求实数
 的取值范围;
的取值范围;当
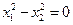 时,求
时,求 的值
的值