空气质量已成为城市居住环境的一项重要指标，空气质量的好坏由空气质量指数确定。空气质量指数越高，代表空气污染越严重：
| 空气质量指数 |
0~35 |
35~75 |
75~115 |
115~150 |
150~250 |
≥250 |
| 空气质量类别 |
优 |
良 |
轻度污染 |
中度污染 |
重度污染 |
严重污染 |
经过对某市空气质量指数进行一个月（30天）监测，获得数据后得到条形图统计图如图：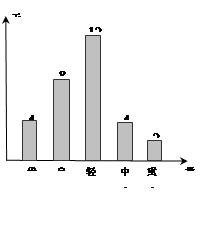
（1）估计某市一个月内空气受到污染的概率（规定：空气质量指数大于或等于75，空气受到污染）；
（2）在空气质量类别为“良”、“轻度污染”、“中度污染”的监测数据中用分层抽样方法抽取一个容量为6的样本，若在这6数据中任取2个数据，求这2个数据所对应的空气质量类别不都是轻度污染的概率.
已知函数
.
（1）证明：不论
为何实数
总为增函数
（2）确定的值, 使为奇函数；
（3）当为奇函数时, 求的值域.
设f(x)为定义在R上的偶函数，当
时，y＝x；当x>2时，y＝f(x)的图像时顶点在P(3,4),且过点A.(2,2)的抛物线的一部分
（1）写出函数f（x）在
上的解析式；
（2）在下面的直角坐标系中直接画出函数f（x）的图像；
（3）写出函数f(x)值域
计算： （1）
（2）
已知集合
，
，
求:（1）
；（2）
已知函数
，
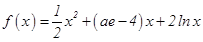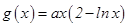（其中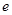
为自然对数的底数，常数
）.
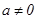（1）若对任意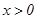
，
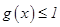恒成立，求正实数
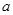的取值范围；
（2）在（1）的条件下，当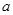取最大值时，试讨论函数
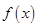在区间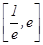
上的单调性；
（3）求证：对任意的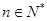
，不等式
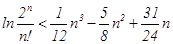成立.