解决下面问题:
如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且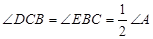 ,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.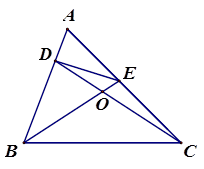
小新同学是这样思考的:
在平时的学习中,有这样的经验:假如△ABC是等腰三角形,那么在给定一组对应条件,如图a,BE,CD分别是两底角的平分线(或者如图b,BE,CD分别是两条腰的高线,或者如图c,BE,CD分别是两条腰的中线)时,依据图形的轴对称性,利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决.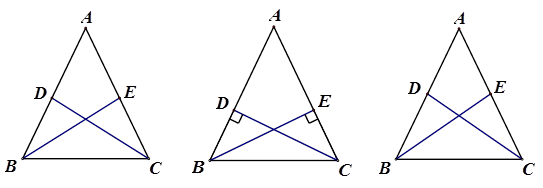
图a 图b 图c
请参考小新同学的思路,解决上面这个问题..
如图所示,在一块长为32米,宽为15米的矩形草地上,在中间要设计一横二竖的供居民散步的小路,要使小路的面积是草地总面积的八分之一,请问小路的宽应是多少米?(注:所有小路进出口的宽度相等,且每段小路均为平行四边形)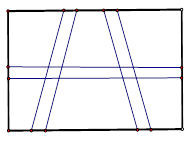
我们知道:对于任何实数 ,①∵
,①∵ ≥0,∴
≥0,∴ +1>0;②∵
+1>0;②∵ ≥0,∴
≥0,∴ +
+ >0.
>0.
模仿上述方法解答:
求证:(1)对于任何实数 ,均有:
,均有: >0;
>0;
(2)不论 为何实数,多项式
为何实数,多项式 的值总大于
的值总大于 的值.
的值.
某种储蓄的月利率是0.36%,今存入本金100元,求本息和(本金与利息的和)y(元)与所存月数x之间的函数关系式,并计算5个月后的本息和.
有一个周长为24的矩形场地,设矩形的一边长为x,另一边长为y(x>y),求y与x的函数关系式,并直接写出自变量x的取值范围。
已知y+b与x+n成正比例(其中b、n是常数).
(1)试说明y是x的一次函数;
(2)若x=3时,y=5,x=2时,y=2,试写出这个函数关系式.