如图,斜四棱柱 的底面
的底面 是矩形,平面
是矩形,平面 ⊥平面
⊥平面 ,
, 分别为
分别为 的中点.
的中点.
求证:
(1) ;(2)
;(2) ∥平面
∥平面 .
.
在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足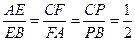 ,将
,将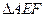 沿EF折起到
沿EF折起到 的位置,使二面角
的位置,使二面角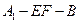 成直二面角,连结
成直二面角,连结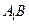 ,
, (如图)(I)求证:
(如图)(I)求证: (Ⅱ)求点B到面
(Ⅱ)求点B到面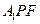 的距离(Ⅲ)求异面直线BP与
的距离(Ⅲ)求异面直线BP与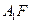 所成角的余弦
所成角的余弦

甲、乙、丙3人投篮,投进的概率分别是 .
.
(Ⅰ)现3人各投篮1次,分别求3人都没有投进和3人中恰有2人投进的概率.
(Ⅱ)用ξ表示乙投篮4次的进球数,求随机变量ξ的概率分布及数学期望Eξ.
在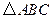 中,角
中,角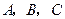 的对边分别为
的对边分别为
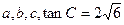 .(I)求
.(I)求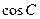 ;(II)若
;(II)若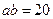 ,且
,且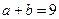 ,求
,求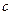 .
.
已知M、N两点的坐标分别是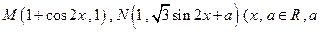 是常数
是常数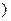 ,令
,令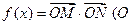 是坐标原点
是坐标原点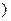 .
.
(Ⅰ)求函数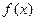 的解析式,并求函数
的解析式,并求函数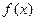 在
在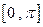 上的单调递增区间;
上的单调递增区间;
(Ⅱ)当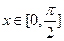 时,
时,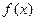 的最大值为
的最大值为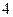 ,求a的值,并说明此时
,求a的值,并说明此时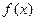 的图象可由函数
的图象可由函数 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到?
已知函数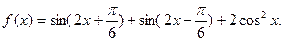
(1)求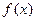 的最大值及最小正周期;
的最大值及最小正周期;
(2)求使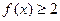 的x的取值范围。
的x的取值范围。