某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
| 指标值分组 |
[90,94) |
[94,98) |
[98,102) |
[102,106) |
[106,110) |
| 频数 |
8 |
20 |
42 |
22 |
8 |
B配方的频数分布表
| 指标值分组 |
[90,94) |
[94,98) |
[98,102) |
[102,106) |
[106,110) |
| 频数 |
4 |
12 |
42 |
32 |
10 |
(1)分别估计用A配方,B配方生产的产品的优质品率;
(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y= 从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
(本小题12分)设直线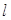 的方程
的方程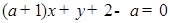
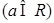 .
.
(1)若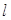 在两坐标轴上截距相等,求
在两坐标轴上截距相等,求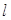
 的一般式方程.
的一般式方程.
(2)若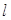 不经过第二象限,求实数
不经过第二象限,求实数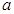 的取值范围.
的取值范围.
(本小题12分)已知两条直线 ,
, ,当
,当 为何值时直线
为何值时直线 与
与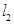 分别有下列关系?
分别有下列关系?
(1)  ⊥
⊥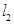 ;
;
(2) ∥
∥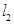
(本小题10分)已知 的三个顶点
的三个顶点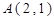 、
、 、
、 ,求
,求
(1) 边所在直线的一般式方程.
边所在直线的一般式方程.
(2) 边上的高
边上的高 所在的直线的一般式方程.
所在的直线的一般式方程.
已知函数 在
在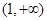 上为增函数,函数
上为增函数,函数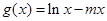
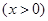 在
在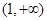 上为减函数.
上为减函数.
(1)分别 求出函数
求出函数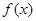 和
和 的导函数;
的导函数;
(2)求实数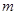 的值;
的值;
(3)求证:当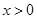 时,
时, 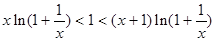
一艘小船在航行中的燃料费和它的速度的立方成正比。已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元。问:此船以多大的速度航行时,能使每公里的费用最少?