如图△ABC中,已知点D在BC边上,且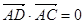 ,
,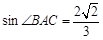 ,
,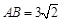 ,
,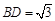 .
.
(1)求AD的长;
(2)求cosC.
在△ABC中,中线长AM=2.
(1)若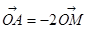 ,求证:
,求证: ;
;
(2)若P为中线AM上的一个动点,求 的最小值.
的最小值.
下表数据是水温度x(℃)对黄酮延长性y(%)效应的试验结果,y是以延长度计算的,且对于给定的x,y为变量.
| x(℃) |
300 |
400 |
500 |
600 |
700 |
800 |
| y(%) |
40 |
50 |
55 |
60 |
67 |
70 |
(1)求y关于x的回归方程;
(2)估计水温度是1 000 ℃时,黄酮延长性的情况.
(可能用到的公式: ,
, ,其中
,其中 、
、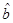 是对回归直线方程
是对回归直线方程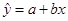 中系数
中系数 、
、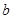 按最小二乘法求得的估计值)
按最小二乘法求得的估计值)
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(1)估计该校学生身高在170~185 cm之间的概率;
(2)从样本中身高在180~190 cm之间的男生中任选2人,求至少有1人身高在185~190 cm之间的概率.
对于函数 与常数a,b,若
与常数a,b,若 恒成立,则称(a,b)为函数
恒成立,则称(a,b)为函数 的一个“P数对”:设函数
的一个“P数对”:设函数 的定义域为
的定义域为 ,且f(1)=3.
,且f(1)=3.
(1)若(a,b)是 的一个“P数对”,且
的一个“P数对”,且 ,
, ,求常数a,b的值;
,求常数a,b的值;
(2)若(1,1)是 的一个“P数对”,求
的一个“P数对”,求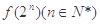 ;
;
(3)若( )是
)是 的一个“P数对”,且当
的一个“P数对”,且当 时,
时,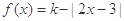 ,求k的值及
,求k的值及 茌区间
茌区间 上的最大值与最小值.
上的最大值与最小值.