对于函数 与常数a,b,若
与常数a,b,若 恒成立,则称(a,b)为函数
恒成立,则称(a,b)为函数 的一个“P数对”:设函数
的一个“P数对”:设函数 的定义域为
的定义域为 ,且f(1)=3.
,且f(1)=3.
(1)若(a,b)是 的一个“P数对”,且
的一个“P数对”,且 ,
, ,求常数a,b的值;
,求常数a,b的值;
(2)若(1,1)是 的一个“P数对”,求
的一个“P数对”,求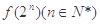 ;
;
(3)若( )是
)是 的一个“P数对”,且当
的一个“P数对”,且当 时,
时,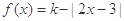 ,求k的值及
,求k的值及 茌区间
茌区间 上的最大值与最小值.
上的最大值与最小值.
已知函数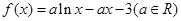 。
。
(Ⅰ)若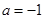 ,求函数
,求函数 的单调区间并比较
的单调区间并比较 与
与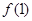 的大小关系
的大小关系
(Ⅱ)若函数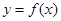 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为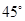 ,对于任意的
,对于任意的 ,函数
,函数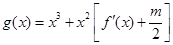 在区间
在区间 上总不是单调函数,求
上总不是单调函数,求 的取值范围;
的取值范围;
(Ⅲ)求证: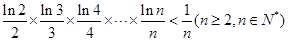 。
。
已知等差数列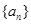 的首项
的首项 ,公差
,公差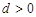 .且
.且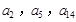 分别是等比数列
分别是等比数列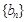 的
的 .
.
(Ⅰ)求数列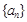 与
与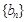 的通项公式;
的通项公式;
(Ⅱ)设数列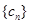 对任意自然数
对任意自然数 均有
均有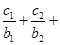 …
… 成立,求
成立,求 …
… 的值.
的值.
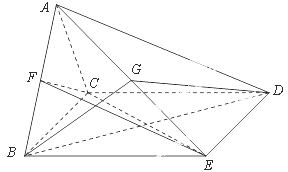
如图,四棱锥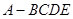 中,
中,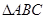 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面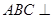 平面
平面 ,
,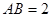 ,
,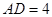 .
.
(Ⅰ)若点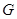 是
是 的中点,求证:
的中点,求证: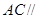 平面
平面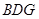 ;
;
(II)试问点 在线段
在线段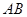 上什么位置时,二面角
上什么位置时,二面角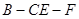 的余弦值为
的余弦值为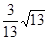 .
.
已知函数 为偶函数,周期为2
为偶函数,周期为2 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若 的值.
的值.
已知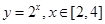 的值域为集合
的值域为集合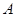 ,
,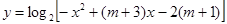 的定义域为集合
的定义域为集合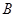 ,其中
,其中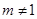 。(1)当
。(1)当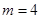 ,求
,求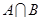 ;(2)设全集为R,若
;(2)设全集为R,若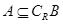 ,求实数
,求实数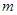 的取值范围.
的取值范围.