袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
已知函数
.
(1)求
在区间
上的最大值;
(2)若过点
存在3条直线与曲线
相切,求
的取值范围;
(3)问过点
分别存在几条直线与曲线
相切?(只需写出结论)
已知椭圆 .
(1)求椭圆C的离心率;
(2)设
为原点,若点
在直线
,点
在椭圆
上,且
,求线段
长度的最小值.
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图: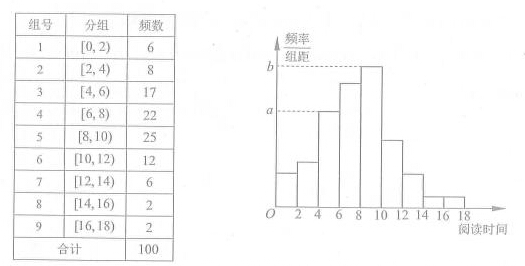
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的
的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
如图,在三棱柱
中,侧棱垂直于底面,
,
,
、
分别为
、
的中点.
(1)求证:平面
平面
;
(2)求证:
平面
;
(3)求三棱锥
的体积.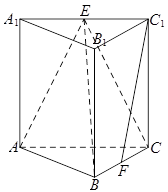
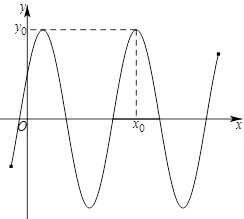
函数
的部分图象如图所示.
(1)写出
的最小正周期及图中
、
的值;
(2)求
在区间
上的最大值和最小值.