在△ABC中,已知tanA=3,sinB= ,求角C的大小.
,求角C的大小.
(满分12分)已知三点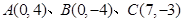 ,
, 外接圆为圆
外接圆为圆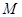 (圆心
(圆心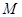 )。
)。
(1)求圆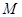 的标准方程;
的标准方程;
(2)若 ,
, 在圆
在圆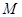 上运动,且
上运动,且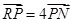 ,求动点
,求动点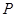 的轨迹方程。
的轨迹方程。
(满分12分)如图三棱锥 中,
中, ,
,
 ,
, ,平面
,平面 平面
平面 。
。
(1) 求证: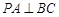 ;
;
(2) 求直线 和面
和面 所成角的正切值。
所成角的正切值。
(满分12分)已知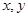 满足直线
满足直线 。
。
(1)求原点 关于直线
关于直线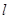 的对称点
的对称点 的坐标;
的坐标;
(2)当 时,求
时,求 的取值范围。
的取值范围。
(满分10分)一个半径为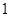 的球内切于一个底面半径为
的球内切于一个底面半径为 的圆锥。
的圆锥。
(1)求圆锥的表面积与球面积之比;
(2)求圆锥的体积与球体积之比。
(本小题满分12分)已知数列 满足
满足 ,
, (
( ).
).
(Ⅰ) 证明数列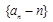 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前n项和为
的前n项和为 ,若对于任意
,若对于任意 ,都满足
,都满足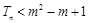 成立,求实数m的取值范围.
成立,求实数m的取值范围.