学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱).
(1)求在1次游戏中:
①摸出3个白球的概率;②获奖的概率.
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).
已知函数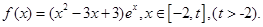
(1)当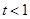 时,求函数
时,求函数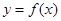 的单调区间;
的单调区间;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间. ,试问函数
,试问函数 在
在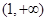 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
已知 为锐角,且
为锐角,且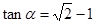 ,函数
,函数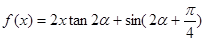 ,数列{
,数列{ }的首项
}的首项 .
.
(1)求函数 的表达式;
的表达式;
(2)求数列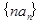 的前
的前 项和
项和 .
.
 的外接圆半径
的外接圆半径 ,角
,角 的对边分别是
的对边分别是 ,且
,且
(1)求角 和边长
和边长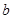 ;
;
(2)求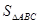 的最大值及取得最大值时的
的最大值及取得最大值时的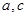 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状.
已知函数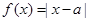 .
.
(1)若 的解集为
的解集为 ,求实数
,求实数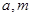 的值.
的值.
(2)当 且
且 时,解关于
时,解关于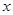 的不等式
的不等式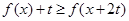 .
.
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.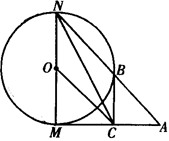
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.