设直线l:x-y+m=0与抛物线C:y2=4x交于不同两点A,B,F为抛物线的焦点.
(1)求△ABF的重心G的轨迹方程;
(2)如果m=-2,求△ABF的外接圆的方程.
已知关于 的不等式:
的不等式: 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.
(1) 求整数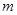 的值;
的值;
(2 )已知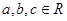 ,若
,若 ,求
,求 的最大值
的最大值
已知曲线 的参数方程为
的参数方程为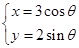 (
(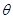 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换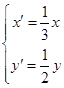 得到曲线
得到曲线 .
.
(1)求曲线 的普通方程;
的普通方程;
(2)若点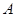 在曲线
在曲线 上,点
上,点
 ,当点
,当点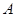 在曲线
在曲线 上运动时,求
上运动时,求 中点
中点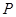 的轨迹方程.
的轨迹方程.
如图,圆 的半径OB垂直于直径AC,M为AO上一点,BM的延长线交
的半径OB垂直于直径AC,M为AO上一点,BM的延长线交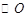 于N,过N点的切线交CA的延长线于P.
于N,过N点的切线交CA的延长线于P.
(1)求证: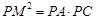 ;
;
(2)若圆 的半径为
的半径为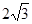 ,
,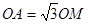 ,求MN的长 .
,求MN的长 .
已知函数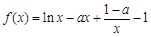 (
(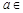
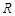 )
)
(1)当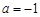 时,求曲线
时,求曲线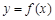 在
在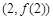 处的切线方程;
处的切线方程;
(2)当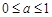 时,试讨论
时,试讨论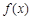 的单调性.
的单调性.
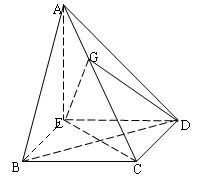
如图,在四棱锥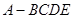 中,
中,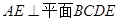 ,
,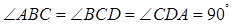 ,
,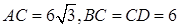 .
.
(1)求证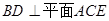 ;
;
(2)设点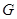 在棱
在棱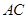 上,且
上,且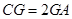 ,试求三棱锥E—GCD的体积.
,试求三棱锥E—GCD的体积.