(本题共6分)将一张正方形纸片剪成四个大小、形状一样的小正方形(如右下图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.请将下表中空缺的数据填写完整,并解答所提出的问题:
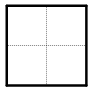
(1)如果剪100次,共能得到__________个正方形.
(2)如果剪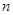 次共能得到
次共能得到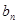 个正方形,试用含有
个正方形,试用含有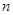 、
、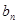 的等式表示它们之间的数量关系.
的等式表示它们之间的数量关系.
______________________________
(3)若原正方形的边长为1,设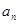 表示第
表示第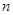 次所剪的正方形的边长,
次所剪的正方形的边长,
①试用含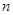 的式子表示
的式子表示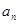 =.
=.
②试猜想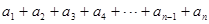 与原正方形边长的数量关系,并用等式写出这个关系:__________________________________________.
与原正方形边长的数量关系,并用等式写出这个关系:__________________________________________.
(本题7分)
(1)当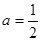 ,
,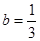 时,分别求代数式①
时,分别求代数式①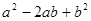 ②
②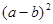 的值;
的值;
(2)当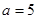 ,
,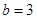 时,分别求代数式①
时,分别求代数式①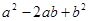 ②
②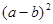 的值;
的值;
(3)观察(1)(2)中代数式的值,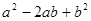 与
与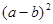 有何关系?
有何关系?
(4)利用你发现的规律,求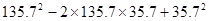 的值.
的值.
(本题5分)某服装店老板以60元的单价购进20件流行款的女服装,老板交代销售小姐以80元为标准价出售.针对不同的顾客,销售小姐对20件服装的售价不完全相同,她把超过80元的记为正数,其销售结果如下表所示: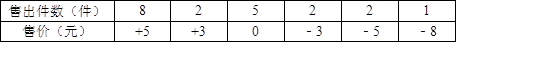
该服装店在售完这20件服装后,请你通过计算说明该服装店老板是赚钱还是亏本?如果赚钱,那么赚了多少钱?如果亏本,那么亏了多少钱?
(本题4分)已知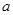 ,
,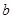 互为倒数,
互为倒数,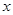 ,
,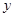 互为相反数,
互为相反数,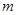 是平方后为4的数.求代数式
是平方后为4的数.求代数式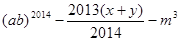 的值.
的值.
(本题6分)已知 ,
, ,
,
(1)求 的值;(结果用x、y表示)
的值;(结果用x、y表示)
(2)当 与
与 互为相反数时,求(1)中代数式的值.
互为相反数时,求(1)中代数式的值.