已知:二次函数
 中的
中的 满足下表:
满足下表:
 |
 |
0 |
1 |
2 |
3 |
||
 |
0 |
 |
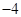 |
 |
 |
(1)求 的值;
的值;
(2)根据上表求 时的
时的 的取值范围;
的取值范围;
(3)若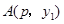 ,
, 两点都在该函数图象上,且
两点都在该函数图象上,且 ,试比较
,试比较 与
与 的大小.
的大小.
某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶,每级小台阶都为0.4米.现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且 .
.
(1)求点D与点C的高度差DH的长度;
(2)求所用不锈钢材料的总长度(即AD+AB+BC).
(结果精确到0.1米.参考数据: ,
, ,
, )
)
如图,⊙P与y轴相切,圆心为P(-2,1),直线MN过点M(2,3),N(4,1).
(1)请你在图中作出⊙P关于y轴对称的⊙P′;(不要求写作法)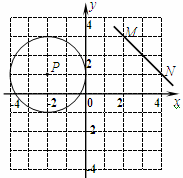
(2)求⊙P在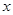 轴上截得的线段长度;
轴上截得的线段长度;
(3)直接写出圆心P′到直线MN的距离.
已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,-3),B(4,0).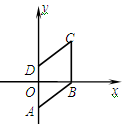
(1)求点D的坐标;
(2)求经过点C的反比例函数解析式.
已知:把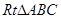 和
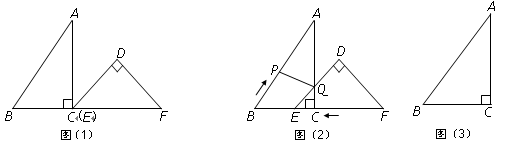
和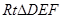 按如图(1)摆放(点
按如图(1)摆放(点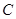 与点
与点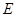 重合),点
重合),点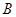 、
、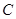 (
(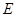 )、
)、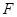 在同一条直线上.
在同一条直线上.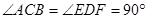 ,
,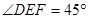 ,
, ,
,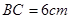 ,
,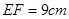 .如图(2),
.如图(2),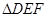 从图(1)的位置出发,以
从图(1)的位置出发,以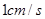 的速度沿
的速度沿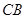 向
向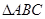 匀速移动,在
匀速移动,在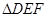 移动的同时,点
移动的同时,点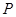 从
从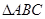 的顶点
的顶点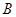 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿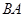 向点
向点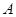 匀速移动.当
匀速移动.当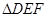 的顶点
的顶点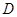 移动到
移动到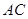 边上时,
边上时,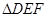 停止移动,点
停止移动,点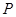 也随之停止移动.
也随之停止移动.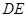 与
与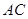 相交于点
相交于点 ,连接
,连接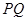 ,设移动时间为
,设移动时间为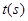
 .
.
(1)当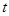 为何值时,点
为何值时,点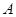 在线段
在线段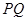 的垂直平分线上?
的垂直平分线上?
(2)连接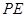 ,设四边形
,设四边形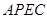 的面积为
的面积为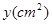 ,求
,求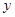 与
与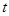 之间的函数关系式;是否存在某一时刻
之间的函数关系式;是否存在某一时刻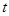 ,使面积
,使面积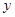 最小?若存在,求出
最小?若存在,求出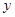 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
(3)是否存在某一时刻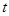 ,使
,使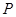 、
、 、
、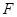 三点在同一条直线上?若存在,求出此时
三点在同一条直线上?若存在,求出此时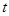 的值;若不存在,说明理由.(图(3)供同学们做题使用)
的值;若不存在,说明理由.(图(3)供同学们做题使用)