已知椭圆C1: +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上,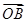 =2
=2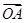 ,求直线AB的方程.
,求直线AB的方程.
已知 .
.
(Ⅰ)化简 ;(Ⅱ)已知
;(Ⅱ)已知 ,求
,求 的值.
的值.
已知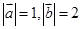
(1)若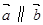 ,求
,求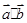 ;
;
(2)若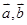 的夹角为
的夹角为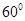 ,求
,求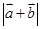 .
.
已知函数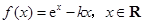
(Ⅰ)若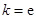 ,试确定函数
,试确定函数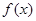 的单调区间;
的单调区间;
(Ⅱ)若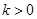 ,且对于任意
,且对于任意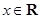 ,
,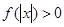 恒成立,试确定实数
恒成立,试确定实数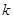 的取值范围;
的取值范围;
(Ⅲ)设函数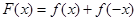 ,求证:
,求证: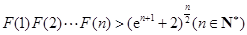 .
.
如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米建立适当的平面直角坐标系,求抛物线方程.现将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少? 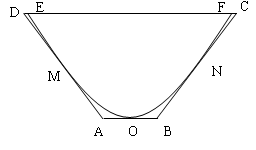
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式 ,其中3<x<6,a 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
,其中3<x<6,a 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
(I)求a的值
(II)若该商品的成品为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大。