已知椭圆 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,直线
的离心率互为倒数,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左焦点为
的左焦点为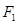 ,右焦点为
,右焦点为 ,直线
,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直 于点
于点 ,线段
,线段 垂直平分线交
垂直平分线交 于点
于点 ,求点
,求点 的轨迹
的轨迹 的方程;
的方程;
(3)设第(2)问中的 与
与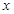 轴交于点
轴交于点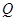 ,不同的两点
,不同的两点 在
在 上,且满足
上,且满足 ,求
,求 的取值范围.
的取值范围.
已知函数 (
( 且
且 ).
).
(1)当 时,求证:
时,求证: 在
在 上单调递增;
上单调递增;
(2)当 且
且 时,求证:
时,求证: .
.
曲线 ,曲线
,曲线 .自曲线
.自曲线 上一点
上一点 作
作 的两条切线切点分别为
的两条切线切点分别为 .
.
(1)若 点的纵坐标为
点的纵坐标为 ,求
,求 ;
;
(2)求 的最大值.
的最大值.
如图,已知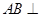 平面
平面 ,
, 为等边三角形.
为等边三角形.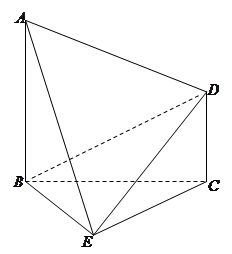
(1)若 ,求证:平面
,求证:平面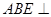 平面
平面 ;
;
(2)若多面体 的体积为
的体积为 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.
在进行一项掷骰子放球游戏中,规定:若掷出1点,甲盒中放一球;
若掷出2点或3点,乙盒中放一球;若掷出4点或5点或6点,丙盒中放一球,前后共掷3
次,设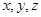 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.
(1)求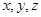 依次成公差大于0的等差数列的概率;
依次成公差大于0的等差数列的概率;
(2)记 ,求随机变量
,求随机变量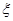 的概率分布列和数学期望.
的概率分布列和数学期望.
在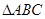 中,
中,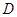 为
为 边上的点
边上的点 ,且
,且 .
.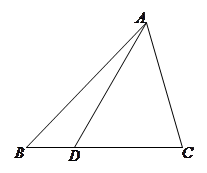
(1)求 ;
;
(2)若 ,求
,求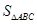 .
.