如图，椭圆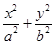
＝1(a＞b＞0)的上，下两个顶点为A，B，直线l：y＝－2，点P是椭圆上异于点A，B的任意一点，连接AP并延长交直线l于点N，连接PB并延长交直线l于点M，设AP所在的直线的斜率为k1，BP所在的直线的斜率为k2.若椭圆的离心率为
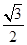，且过点A(0,1)．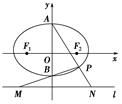
(1)求k1·k2的值；
(2)求MN的最小值；
(3)随着点P的变化，以MN为直径的圆是否恒过定点？若过定点，求出该定点；如不过定点，请说明理由．
某民营企业生产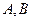
两种产品
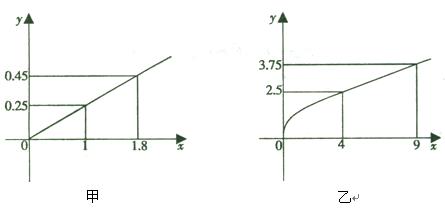
，根据市场调查与预测，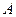
产品的利润与投资成正比，其关系如图甲，
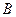产品的利润与投资的算术平方根成正比，其关系如图乙(注：利润与投资单位：万元)
．
（Ⅰ）分别将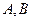两种产品的利润表示为投资
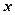(万元)的函数关系式；
（Ⅱ）该企业已筹集到10万元资金，并
全部投入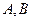两种产品的生产，问：怎样分配这10万元投资，才能使企业获得最大利润，其最大
利润为多少万元?
已知曲线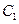
：
（
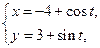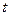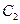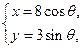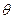为参数），
：
（
为参数）.
（Ⅰ）将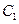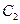，的方程化为普通方程；
（Ⅱ）若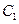上的点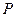
对应的参数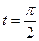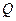为
，
为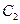上的动点，求
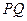中点
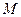到直线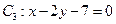
距离的最小值.
已知二阶矩阵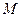
有特征值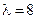
及对应的一个特征向量
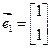，并且矩阵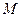对应的变换将点
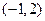变换成
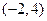.求矩阵.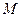
（Ⅰ）把点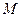
的直角坐标化为极坐标；
（Ⅱ）求圆心在极轴上,且过极点和点
的圆的极坐标方程.
（本小题满分10分）选修4—5：不等式选讲。设正有理数
是
的一个近似值，令
．
（I）若
，求证：
；
（II）求证：
比更接近于．