已知函数f(x)=-x3+x2,g(x)=aln x,a∈R.
(1)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求a的取值范围;
(2)设F(x)=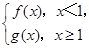 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
如图,椭圆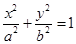 上的点M与椭圆右焦点
上的点M与椭圆右焦点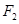 的连线
的连线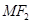 与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
(1)求椭圆的离心率;
(2)F1是椭圆的左焦点,C是椭圆上的任一点,证明: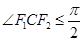 ;
;
(3)过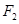 且与AB垂直的直线交椭圆于P、Q,若
且与AB垂直的直线交椭圆于P、Q,若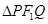 的面积是20
的面积是20 ,求此时椭圆的方程.
,求此时椭圆的方程.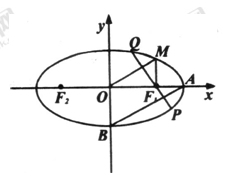
设函数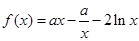 .
.
(1)若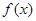 在
在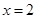 时有极值,求实数
时有极值,求实数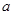 的值和
的值和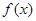 的极大值;
的极大值;
(2)若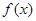 在定义域上是增函数,求实数
在定义域上是增函数,求实数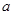 的取值范围.
的取值范围.
已知椭圆C的两焦点分别为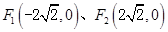 ,长轴长为6,
,长轴长为6,
⑴求椭圆C的标准方程;
⑵已知过点(0,2)且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度。.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1。
(1)请在线段CE上找到一点F,使得直线BF∥平面ACD,并证明;
(2)求平面BCE与平面ACD所成锐二面角的大小;
在数列{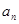 }中,
}中,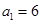 ,且
,且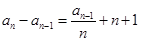
 ,
,
(1)求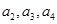 的值;
的值;
(2)猜测数列{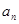 }的通项公式,并用数学归纳法证明。
}的通项公式,并用数学归纳法证明。