已知:如图,∠1=∠2,∠C=∠D,求证:AC=AD. 
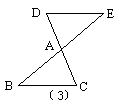
(阅读与探究)如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角. 


(探究题)如图所示,△ABC绕顶点A顺时针旋转,若∠B=40°,∠C=30°.
(1)顺时针旋转多少度时,旋转后的△AB'C'的顶点C'与原三角形的顶点B和A在同一直线上?(原△ABC是指开始位置)
(2)再继续旋转多少度时,点C、A、C'在同一直线上?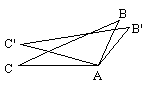
如图所示,用同样粗细,同种材料的金属构制两个全等三角形,△ABC和△DEF,已知∠B=∠E,∠C=∠F,AC的质量为25克,EF的质量为30克,求金属丝AB的质量的取值范围. 
如图所示,△ABC≌△AEC,B和E是对应顶点,∠B=30°,∠ACB=85°,求△AEC各内角的度数. 