如图,已知二次函数y=x -4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
-4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
(1)求直线BC的解析式;
(2)点D是在直线BC下方的抛物线上的一个动点,当△BCD的面积最大时,求D点坐标.
将一幅三角板Rt△ABC和Rt△DEF按如图1摆放,点E, A, D, B在一条直线上,且D是AB的中点,将Rt△DEF绕点D顺时针方向旋转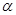 (0°<
(0°<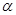 <90°)角,在旋转过程中,直线DE与AC相交于点M,直线DF与BC相交于点N,分别过点M, N作直线AB的垂线,垂足分别为G, H.
<90°)角,在旋转过程中,直线DE与AC相交于点M,直线DF与BC相交于点N,分别过点M, N作直线AB的垂线,垂足分别为G, H.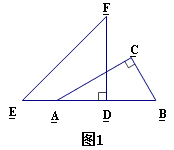
(1)当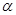 =30°时(如图2),求证:AG=DH;
=30°时(如图2),求证:AG=DH;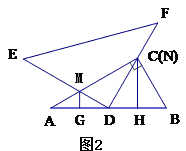
(2)当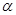 =60°时(如图3),(1)中的结论是否仍成立?请写出你的结论,并说明理由.
=60°时(如图3),(1)中的结论是否仍成立?请写出你的结论,并说明理由.
如图,在平面直角坐标系中,以点M(0, )为圆心,作⊙M交x轴于A、B两点,交y轴于C、D两点,连结AM并延长交⊙M于点P,连结PC交x轴于点E,连结DB,∠BDC=30°.
)为圆心,作⊙M交x轴于A、B两点,交y轴于C、D两点,连结AM并延长交⊙M于点P,连结PC交x轴于点E,连结DB,∠BDC=30°.

(1)求弦AB的长;
(2)求直线PC的函数解析式;
(3)连结AC,求△ACP的面积.
已知一元二次方程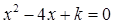 有两个实数根.
有两个实数根.
(1)求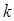 的取值范围;
的取值范围;
(2)如果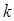 是符合条件的最大整数,且一元二次方程
是符合条件的最大整数,且一元二次方程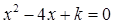 与
与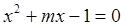 有一个相同的根,求此时
有一个相同的根,求此时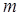 的值.
的值.
美化城市,改善人们的居住环境已成为城市建设的一项重要内容,南沙区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿化面积不断增加(如图所示)
(1)根据图中所提供的信息,回答下列问题:2011年的绿化面积为 公顷,比2010年增加了 公顷。
(2)为满足城市发展的需要,计划到2013年使城区绿化地总面积达到72.6公顷,试求这两年(2011~2013)绿地面积的年平均增长率。
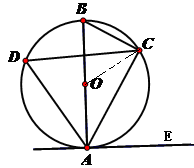
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,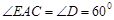 .
.
(1)求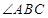 的度数;
的度数;
(2)求证:AE是⊙O的切线。