在xoy平面直角坐标系的第Ⅰ象限有射线OA，OA与x轴正方向夹角为30°，如图所示，OA与y轴所夹区域存在y轴负方向的匀强电场，其它区域存在垂直坐标平面向外的匀强磁场；有一带正电粒子质量m，电量q，从y轴上的P点沿着x轴正方向以大小为v0的初速度射入电场，运动一段时间沿垂直于OA方向经过Q点进入磁场，经磁场偏转，过y轴正半轴上的M点再次垂直进入匀强电场。已知OP = h，不计粒子的重力。
⑴ 求粒子垂直射线OA经过Q点的速度vQ；
⑵ 求匀强电场的电场强度E与匀强磁场的磁感应强度B的比值；
⑶ 粒子从M点垂直进入电场后，如果适当改变电场强度，可以使粒子再次垂直OA进入磁场，再适当改变磁场的强弱，可以使粒子再次从y轴正方向上某点垂直进入电场；如此不断改变电场和磁场，会使粒子每次都能从y轴正方向上某点垂直进入电场，再垂直OA方向进入磁场……，求粒子从P点开始经多长时间能够运动到O点？
如图所示，水平向左做匀变速直线运动的车厢中，悬挂一个小球质量m=1kg，悬线与竖直方向的夹角为30° 球和车厢相对静止，车厢底部有一质量为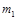
="2" kg的木块，木块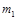则始终相对于车厢静止,求：（g＝10m/s2）
车厢运动的加速度大小和方向
悬线对小球的拉力
木块受到的摩擦力的大小和方向
一石子从楼顶由静止开始下落，不计空气阻力，现测得石子落地时的速度是30m/s， 求石子下落的时间？
楼有多高？（g=10m/s2）
如图甲所示，水平加速电场的加速电压为U0，在它的右侧有由水平正对放置的平行金属板a、b构成的偏转电场，已知偏转电场的板长L="0.10" m，板间距离d=5.0×10-2 m，两板间
接有如图15乙所示的随时间变化的电压U，且a板
电势高于b板电势。在金属板右侧存在有界的匀强磁场，磁场的左边界为与金属板右侧重合的竖直平面MN，MN右侧的磁场范围足够大，磁感应强度B=5.0×10-3T，方向与偏转电场正交向里（垂直纸面向里）。质量和电荷量都相同的带正电的粒子从静止开始经过电压U0=50V的加速电场后，连续沿两金属板间的中线OO′方向射入偏转电场中，中线OO′与磁场边界MN垂直。已知带电粒子的比荷
=1.0×108 C/kg，不计粒子所受的重力和粒子间的相互作用力，忽略偏转电场两板间电场的边缘效应，在每个粒子通过偏转电场区域的极短时间内，偏转电场可视作恒定不变。
求t=0时刻射入偏转电场的粒子在磁场边界上的入射点和出射点间的距离；
求粒子进入磁场时的最大速度；
对于所有进入磁场中的粒子，如果要增大粒子在磁场边界上的入射点和出射点间的距离，应该采取哪些措施？试从理论上推理说明。
1879年美国物理学家霍尔在研究载流导体在磁场中受力情况时，发现了一种新的电磁效应：将导体置于磁场中，并沿垂直磁场方向通入电流，则在导体中垂直于电流和磁场的方向会产生一个横向电势差，这种现象后来被称为霍尔效应，这个横向的电势差称为霍尔电势差。
如图甲所示，某长方体导体abcda′b′c′d′的高度为h、宽度为l，其中的载流子为自由电子，其电荷量为e，处在与ab b′a′面垂直的匀强磁场中，磁感应强度为B0。在导体中通有垂直于bcc′b′面的电流，若测得通过导体的恒定电流为I，横
向霍尔电势差为UH，求此导体中单位体积内自由电子的个数。对于某种确定的导体材料，其单位体积内的载流子数目n和载流子所带电荷量q均为定值，人们将H=
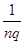定义为该导体材料的霍尔系数。利用霍尔系数H已知的材料可以制成测量磁感应强度的探头，有些探头的体积很小，其正对横截面（相当于图14甲中的ab b′a′面）的面积可以在0.1cm2以下，因此可以用来较精确的测量空间某一位置的磁感应强度。如图14乙所示为一种利用霍尔效应测磁感应强度的仪器，其中的探头装在探杆的前端，且使探头的正对横截面与探杆垂直。这种仪器既可以控制通过探头的恒定电流的大小I，又可以监测出探头所产生的霍尔电势差UH，并自动计算出探头所测位置磁场的磁感应强度的大小，且显示在仪器的显示窗内。
①在利用上述仪器测量磁感应强度的过程中，对探杆的放置方位有何要求；
②要计算出所测位置磁场的磁感应强度，除了要知道H、I、UH外，还需要知道哪个物理量，并用字母表示。推导出用上述这些物理量表示所测位置磁感应强度大小的表达式。
在如图所示的电路中，两平行正对金属板A、B水平放置，两板间的距离d=4.0cm。电源电动势E=400V，内电阻r=20Ω，电阻R1=1980Ω。闭合开关S，待电路稳定后，将一带正电的小球（可视为质点）从B板上的小孔以初速度v0=1.0m/s竖直向上射入两板间，小球恰好能到达A板。若小球所带电荷量q=1.0×10-7C，质量m=2.0×10-4kg，不考虑空气阻力，忽略射入小球对电路的影响，取g=10m/s2。求：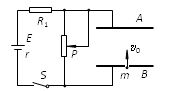
A、
B两金属板间的电压的大小U；滑动变阻器消耗的电功率P滑；
电源的效率η。