一石子从楼顶由静止开始下落,不计空气阻力,现测得石子落地时的速度是30m/s, 求石子下落的时间?
楼有多高?(g=10m/s2)
如图所示,空间存在两个匀强磁场,它们分界线是边长为3L的等边三角形APC,D、E、F三点分别在PC、CA、AP边上,AF = PD = CE = L,分界线两侧的磁场方向相反且垂直于纸面,磁感应强度大小相同,均为B,分界线外的磁场区域足够大。现有一质量为m、电荷量为q的带正电离子(不计重力),从F点以速度v向三角形内射入。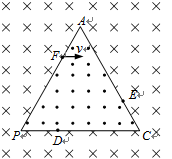
(1)如果速度v方向与PC边平行,离子第一次到分界线就经过D点,则磁感应强度B的大小是多少?
(2)如果改变磁感应强度B的大小和速度v的方向(速度v的方向均在纸平面内),使离子第一次、第二次到达分界线时依次经过D点和E点,求离子周期性运动的周期。
(3)再改变磁感应强度B的大小和速度v的方向(速度v的方向均在纸平面内),能否仍使离子第一次、第二次到达分界线时依次经过D点和E点?为什么?
如图所示, 金属导轨是由倾斜和水平两部分圆滑相接而成, 倾斜部分与水平夹角q=37°,导轨电阻不计。abcd矩形区域内有垂直导轨平面的匀强磁场,bc = ad = s =" 0.20" m。导轨上端搁有垂直于导轨的两根相同金属杆P1、P2,且P1位于ab与P2的中间位置,两杆电阻均为R,它们与导轨的动摩擦因数m=" 0.30," P1杆离水平轨道的高度h =" 0.60m," 现使杆P2不动,让P1杆静止起滑下,杆进入磁场时恰能做匀速运动,最后P1杆停在AA¢位置。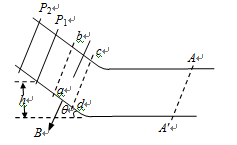
求: (1)P1杆在水平轨道上滑动的距离x。
(2)P1杆停止后, 再释放P2杆, 为使P2杆进入磁场时也做匀速运动, 事先要把磁场的磁感应强度大小调为原来的多少倍?
(3)若将磁感应强度B调为原来3倍, 再释放P2, 问
P2杆是否有可能与P1杆不碰撞? 为什么?
在公路的十字路口, 红灯拦停了很多汽车, 拦停的汽车排成笔直的一列, 最前面的一辆汽车的前端刚好与路口停车线相齐, 相邻两车的前端之间的距离均为l =" 6.0" m,若汽车起动时都以a =2.5m/s2 的加速度作匀加速运动, 加速到v="10.0" m/s 后做匀速运动通过路口。该路口亮绿灯时间t =" 40.0" s, 而且有按倒计时显示的时间显示灯. 另外交通规则规定: 原在绿灯时通行的汽车, 红灯亮起时, 车头已越过停车线的汽车允许通过。请解答下列问题:
(1)若绿灯亮起瞬时, 所有司机同时起动汽车, 问有多少辆汽车能通过路口?
(2)第(1)问中, 不能通过路口的第一辆汽车司机, 在时间显示灯刚亮出“3”时开始刹车做匀减速运动, 结果车的前端与停车线相齐时刚好停下, 求刹车后汽车加速度大小。
(3)事实上由于人反应时间的存在, 绿灯亮起时不可能所有司机同时起动汽车。现假设绿灯亮起时, 第一个司机迟后Dt=0.90s起动汽车, 后面司机都比前一辆车迟后0.50s起动汽车, 在该情况下, 有多少辆车能通过路口?
某科技活动小组同学, 用下如下图甲的实验器材, 测绘一个非线性电学元件的伏安特性曲线, 其中电压表内阻约20KΩ,毫安表内阻约200Ω, 滑动变阻器最大阻值为100W, 电源能提供的电压为9V。实验测得该元件两端电压U和通过它的电流I的数据如下表所示: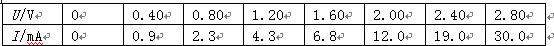
(1) 根据表中的数据可获得的信息及有关电学实验的知识, 请在右边的方框中画出该活动小组采用的实验电路图。
(2) 图甲是尚未完成连接的电路, 请你把其连接完整。
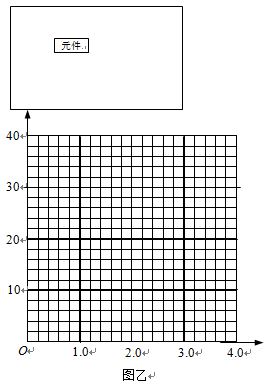
(3) 根据表中数据,在图乙的坐标纸中画出该元件的伏安特性曲线。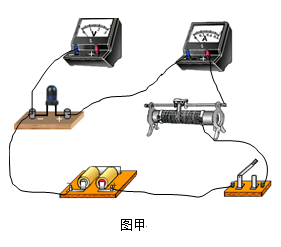
如图所示,一个质量为m=0.6kg的小球,在左侧平台上运行一段距离后从边缘A点以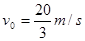 水平飞出,恰能沿切线从P点进入竖直圆弧管道并继续滑行。已知管道口径远小于圆弧半径,OP与竖直方向的夹角是37°,平台到地面的高度差为h=1.45m。若小球运动到圆弧轨道最低点时的速度大小是 10m/s。取g=10m/s2,sin53°=0.8,cos53°=0.6。求:
水平飞出,恰能沿切线从P点进入竖直圆弧管道并继续滑行。已知管道口径远小于圆弧半径,OP与竖直方向的夹角是37°,平台到地面的高度差为h=1.45m。若小球运动到圆弧轨道最低点时的速度大小是 10m/s。取g=10m/s2,sin53°=0.8,cos53°=0.6。求: 
(1)P点距地面的高度
(2)圆弧轨道最低点对小球支持力的大小
(3)若通过最高点Q点时小球对外管壁的压力大小9N,则小球经过Q点时的速度大小是多少?