在如图所示的竖直平面内,物体A和带正电的物体B用跨过定滑轮的绝缘轻绳连接,分别静止于倾角θ=37°的光滑斜面上的M点和粗糙绝缘水平面上,轻绳与对应平面平行.劲度系数k=5 N/m的轻弹簧一端固定在O点,一端用另一轻绳穿过固定的光滑小环D与A相连,弹簧处于原长,轻绳恰好拉直,DM垂直于斜面.水平面处于场强E=5×104 N/C、方向水平向右的匀强电场中.已知A、B的质量分别为mA=0.1 kg和mB=0.2 kg,B所带电荷量q=+4×10-6 C.设两物体均视为质点,不计滑轮质量和摩擦,绳不可伸长,弹簧始终在弹性限度内,B电荷量不变.取g=10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)求B所受静摩擦力的大小;
(2)现对A施加沿斜面向下的拉力F,使A以加速度a=0.6 m/s2开始做匀加速直线运动.A从M到N的过程中,B的电势能增加了ΔEp=0.06 J.已知DN沿竖直方向,B与水平面间的动摩擦因数μ=0.4.求A到达N点时拉力F的瞬时功率.
有一根弹簧,用5N的力拉它,总长度为12cm;若用10N的力拉它,总长度为14cm,求弹簧的原长为多少?
如图所示,在倾角为θ的粗糙斜面上,有一个质量为m的物体被水平力F推着静止于斜面上,已知物体与斜面间的动摩擦因数为μ,且μ<tanθ,若物体恰好不下滑,则推力F为多少?若物体恰好不上滑,则推力F为多少?(最大静摩擦力等于滑动摩擦力)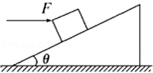
1935年在苏联的一条直铁轨上,有一列火车因蒸汽不足而停驶,驾驶员把货车厢甲(如图所示)留在现场,只拖着几节车厢向前方不远的车站开进,但他忘了将货车厢刹好,使车厢在斜坡上以4m/s的速度匀速后退,此时另一列火车乙正以16m/s的速度向该货车厢驶来.驾驶技术相当好的驾驶员波尔西列夫发现货车厢甲向自己驶来时两车相距仅100m,他立即刹车,紧接着加速倒退,结果恰好接住了货车厢甲,从而避免了相撞.设列车乙刹车过程和加速倒退过程均为匀变速直线运动,且加速度大小相等,求列车乙刹车和加速倒退过程的加速度大小.
在正常情况下,火车以54km/h的速度匀速开过一个小站.现因需要,必须在这一小站停留,火车将要到达小站时,以﹣0.5m/s2的加速度做匀减速运动,停留2分钟后,又以0.3m/s2的加速度出小站,一直到恢复原来的速度.求因列车停靠小站而延误的时间.
为了人文关怀,保障市民出行安全和严格执法,各大城市交管部门强行推出”电子眼”,据了解,在城区内全方位装上”电子眼”后立马见效,机动车擅自闯红灯的大幅度减少,减少了交通事故的发生.现有甲、乙两汽车正沿同一平直马路同向匀速行驶,甲车在前乙车在后,速度均为10m/s.当两车快要到一十字路口时,甲车司机看到绿灯已转换为黄灯,于是紧急刹车(反应时间忽略不计),乙车司机为了避免与甲车相撞也紧急刹车,但乙车司机反应较慢(反应时间为0.5s).已知甲车紧急刹车时的加速度是4m/s2,乙车紧急刹车时的加速度是5m/s2求:
(1)若甲车司机看黄灯时车头距警戒线15m,他采取上述措施能否避免闯红灯?
(2)为了保证两车在紧急刹车过程中不相撞,甲、乙两汽车行驶过程中应保持多大距离?