如图,在梯形ABCD中,AD//BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.连接BF、AC.
(1)求证:四边形ABFC是平行四边形;
(2)如果DE2=BE·CE,求证四边形ABFC是矩形.
在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),
(1)若将△AOB绕点O逆时针旋转90°得到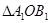 ,请在图中画出
,请在图中画出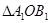 ,并写出点
,并写出点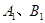 的坐标;
的坐标;
(2)若将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F. 请在图中画出△AEF,并写出点E,F的坐标.
用适当的方法解方程: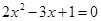 .
.
如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).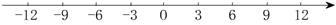
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
关于x的方程 与
与 的解互为相反数.
的解互为相反数.
(1)求m的值;
(2)求这两个方程的解.
两种移动电话记费方式表
(1)一个月内本地通话多少分钟时,两种通讯方式的费用相同?
(2)若某人预计一个月内使用本地通话费180元,则应该选择哪种通讯方式较合算?
| 全球通 |
神州行 |
|
| 月租费 |
50元/分 |
0 |
| 本地通话费 |
0.40元/分 |
0.60元/分 |