某相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品,根据市场调研,发现如下两种信息:
信息一:销售甲款护肤品所获利润y(元)与销售量x(件)之间存在二次函数关系y=ax2+bx.在x=10时,y=140;当x=30时,y=360.
信息二:销售乙款护肤品所获利润y(元)与销售量x(件)之间存在正比例函数关系y=3x.请根据以上信息,解答下列问题;
(1)求信息一中二次函数的表达式;
(2)该相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品共100件,请设计一个营销方案,使销售甲、乙两款护肤品获得的利润之和最大,并求出最大利润.
在由m×n(m×n>1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数f,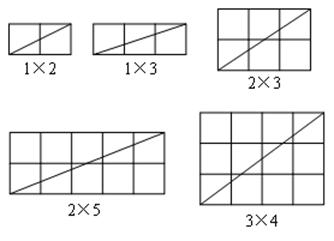
(1)当m、n互质(m、n除1外无其他公因数)时,观察下列图形并完成下表:
| m |
n |
m+n |
f |
| 1 |
2 |
3 |
2 |
| 1 |
3 |
4 |
3 |
| 2 |
3 |
5 |
4 |
| 2 |
5 |
6 |
|
| 3 |
5 |
7 |
猜想:当m、n互质时,在m×n的矩形网格中,一条对角线所穿过的小正方形的个数f与m、n的关系式是______________________________(不需要证明);
(2)当m、n不互质时,请画图验证你猜想的关系式是否依然成立,
在平面直角坐标系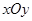 中,A、B为反比例函数
中,A、B为反比例函数
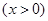 的图象上两点,A点的横坐标与B点的纵坐标均为1,将
的图象上两点,A点的横坐标与B点的纵坐标均为1,将
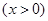 的图象绕原点O顺时针旋转90°,A点的对应点为
的图象绕原点O顺时针旋转90°,A点的对应点为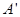 ,B点的对应点为
,B点的对应点为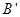 .
.
(1)求旋转后的图象解析式;
(2)求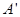 、
、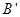 点的坐标;
点的坐标;
(3)连结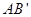 .动点
.动点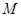 从
从 点出发沿线段
点出发沿线段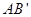 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点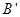 运动;动点
运动;动点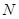 同时从
同时从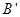 点出发沿线段
点出发沿线段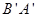 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点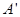 运动,当其中一个点停止运动时另一个点也随之停止运动.设运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设运动的时间为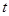 秒,试探究:是否存在使
秒,试探究:是否存在使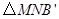 为等腰直角三角形的
为等腰直角三角形的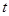 值,若存在,求出
值,若存在,求出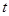 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图1,在□ABCD中,AE⊥BC于E,E恰为BC的中点,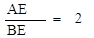 .
.
(1)求证:AD=AE;
(2)如图2,点P在BE上,作EF⊥DP于点F,连结AF. 求证: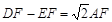 ;
;
(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.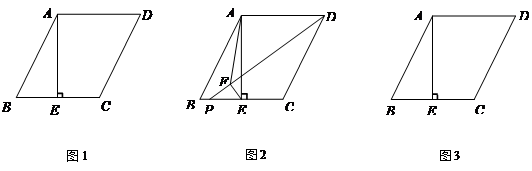
如图,已知一次函数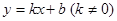 的图象与
的图象与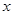 轴、
轴、 轴分别交于A、B两点且与反比例函数
轴分别交于A、B两点且与反比例函数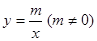 的图象在第一象限交于C点,CD⊥
的图象在第一象限交于C点,CD⊥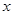 轴于D点,若∠C A D=
轴于D点,若∠C A D=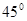 ,A B =
,A B = 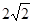 ,C D =
,C D = 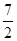
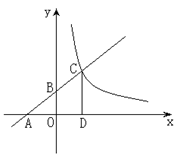
(1)求点A、B、D的坐标
(2)求一次函数的解析式
(3)反比例函数的解析式
(4)求△BCD的面积
如图8-1、9-1,现将二张形状、大小完全相同的平行四边形透明纸片,分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形纸片的每个顶点与小正方形的顶点重合.分别在图8-1、图9-1中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,按所采裁图形的实际大小,在图8-2中拼成正方形,在图9-2中拼成一个角是135° 的三角形.
要求:
(1)裁成的两部分在拼成几何图形时要互不重叠且不留空隙;
(2)所拼出的几何图形的各顶点必须与小正方形的顶点重合.