已知函数f(x)=sin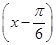 +cosx-
+cosx- ,g(x)=2sin2
,g(x)=2sin2 .
.
(1)若α是第一象限角,且f(α)=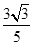 .求g(α)的值;
.求g(α)的值;
(2)求使f(x)≥g(x)成立的x的取值集合.
已知椭圆C的两焦点分别为 ,长轴长为6,
,长轴长为6,
(1)求椭圆C的标准方程;
(2)已知过点(0,0)且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度
(满分14 分)已知抛物线 ,焦点为F,顶点为原点O,
,焦点为F,顶点为原点O,
(1)求抛物线的焦点坐标准线方程;
(2)若P(a,4),求Q到F的距离;
(3)若点P在抛物线上移动,M是OP的中点,求点M的轨迹方程.
(满分14 分)已知椭圆 的两焦点是
的两焦点是 ,P是椭圆上的一点
,P是椭圆上的一点
(1)求椭圆的实轴的长和焦点坐标;
(2)若 求
求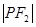 的长;
的长;
(3)一双曲线与椭圆有公共焦点,且以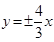 为渐近线,求此双曲线的标准方程。
为渐近线,求此双曲线的标准方程。
(本小题满分14分)求圆心在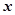 轴上
轴上 且过点A(-1,4)、B(6,-3)圆的方程
且过点A(-1,4)、B(6,-3)圆的方程
(满分12分)已知数列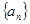 、
、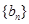 :(1)若
:(1)若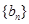 是等比数列,且
是等比数列,且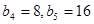 ,求其通项公式
,求其通项公式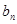 。(2)若
。(2)若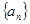 为等差数列,且
为等差数列,且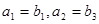 ,求其前15项的和
,求其前15项的和 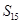 .
.