(本小题满分14分)求圆心在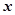 轴上
轴上 且过点A(-1,4)、B(6,-3)圆的方程
且过点A(-1,4)、B(6,-3)圆的方程
已知函数 (
( )
)
(1)求 的定义域;
的定义域;
(2)问是否存在实数 、
、 ,当
,当 时,
时, 的值域为
的值域为 ,且
,且 若存在,求出
若存在,求出 、
、 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知全集U=R,非空集合 <
< ,
, <
< .
.
(1)当 时,求
时,求 ;
;
(2)命题 ,命题
,命题 ,若q是p的必要条件,求实数a的取值范围.
,若q是p的必要条件,求实数a的取值范围.
设定义域为[0,1]的函数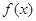 同时满足以下三个条件时称
同时满足以下三个条件时称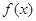 为“友谊函数”:
为“友谊函数”:
(1)对任意的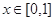 ,总有
,总有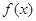 ≥0;
≥0;
(2) ;
;
(3)若 成立,则下列判断正确的有 .
成立,则下列判断正确的有 .
(1)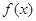 为“友谊函数”,则
为“友谊函数”,则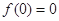 ;
;
(2)函数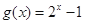 在区间[0,1]上是“友谊函数”;
在区间[0,1]上是“友谊函数”;
(3)若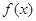 为“友谊函数”,且0≤
为“友谊函数”,且0≤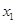 <
< ≤1,则
≤1,则 ≤
≤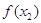 .
.
已知函数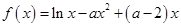 .
.
(1)若 在
在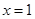 处取得极值,求实数
处取得极值,求实数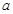 的值;
的值;
(2)求函数 在区间
在区间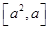 上的最大值.
上的最大值.
在圆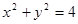 上任取一点
上任取一点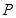 ,设点
,设点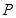 在
在 轴上的正投影为点
轴上的正投影为点 .当点
.当点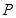 在圆上运动时,动点
在圆上运动时,动点 满足
满足 ,动点
,动点 形成的轨迹为曲线
形成的轨迹为曲线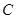 .
.
(1)求曲线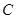 的方程;
的方程;
(2)已知点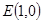 ,若
,若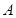 、
、 是曲线
是曲线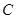 上的两个动点,且满足
上的两个动点,且满足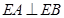 ,求
,求 的取值范围.
的取值范围.