已知a=(sin α,sin β),b=(cos(α-β),-1),c=(cos(α+β),2),α,β≠kπ+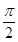 (k∈Z).
(k∈Z).
(1)若b∥c,求tan α·tan β的值;
(2)求a2+b·c的值.
(本小题分14分)已知函数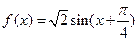
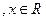
(Ⅰ)求 的最小正周期T;
的最小正周期T;
(Ⅱ)求 的最大值和最小值;
的最大值和最小值;
(Ⅲ)求当 取最大值时
取最大值时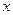 值的集合。
值的集合。
(本小题满分14分)已知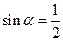 , (1)求角
, (1)求角 所在象限;(2)求
所在象限;(2)求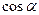 及
及 的值。
的值。
已知函数 ,
,
(1)求函数的定义域及值域;
(2)判断该函数的奇偶性,并证明你的结论.
(本小题满分14分)已知圆C: ,
,
(1)求出此圆圆心C的坐标和半径r;
(2)求直线y=x被圆C所截得的弦长.
(本小题满分14分)已知x,y之间的一组数据如下表:
| x |
1 |
3 |
6 |
7 |
8 |
| y |
1 |
2 |
3 |
4 |
5 |
(1)以x为横坐标,y为纵坐标在直角坐标系中画出散点图,并说明这两个变量之间的关系是正相关关系还是负相关关系。
(2)求线性回归方程.