某居民小区有两个相互独立的安全防范系统(简称系统)A和B，系统A和B在任意时刻发生故障的概率分别为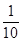
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为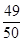
，求p的值；
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ，求ξ的概率分布列及数学期望Eξ.
已知函数f(x)＝x2－4，设曲线y＝f(x)在点(xn，f(xn))
处的切线与x轴的交点为(xn＋1,0)(n∈N＋)，其中x1为正实数．
(1)用xn表示xn＋1；
(2)求证：对一切正整数n，xn＋1≤xn的充要条件是x1≥2；
(3)若x1＝4，记an＝lg 
，证明数列{an}成等比数列，并求数列{xn}的通项公式．
用数学归纳法证明：对任意n∈N＋，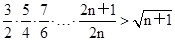
成立．
观察下表：
1，
2,3
4,5,6,7
8,9,10,11,12,13,14,15，
…
问：(1)此表第n行的最后一个数是多少？
(2)此表第n行的各个数之和是多少？
(3)2 008是第几行的第几个数？
设a>0，b>0,2c>a＋b，求证：
(1)c2>ab；
(2)c－
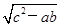<a<c＋.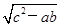
(本小题满分13分)下列是真命题还是假命题，用分析法证明你的结论．
命题：若a>b>c且a＋b＋c＝0，则
.