已知多项式f(n)= n5+
n5+ n4+
n4+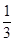 n3-
n3- n.
n.
(1)求f(-1)及f(2)的值;
(2)试探求对一切整数n,f(n)是否一定是整数?并证明你的结论.
有10名教师,其中男教师6名,女教师4名
(1)现要从中选2人去参加会议,有多少种不同的选法?
(2)现要从中选出男、女教师各两名去参加会议,有多少种不同的选法?
解方程: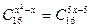
A,B,C,D,E五人站成一排:
(1)A,B两人相邻的不同排法有多少种?
(2)A,B,C两两不相邻的排法有多少种?
(3)A,B都与C相邻的不同排法种数有多少种?
(4)A,B,C顺序一定的排法有多少种?
计划展出10幅不同的画,其中1幅水彩画,4幅油画,5幅国画,排成一行陈列,要求同一品种的画必须放在一起,并且水彩画不放在两端,不同的陈列种数有多少种?
2个男生和4个女生排成一排,其中男生既不相邻也不排两端的不同排法共有多少种?