求使等式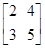
＝
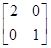M
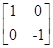成立的矩阵M.
（满分14分）已知函数
,（
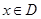），若同时满足以下条件：
①在D上单调递减或单调递增；
②存在区间[
]
D,使在[]上的值域是[]，那么称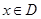（）为闭函数．
（1）求闭函数
符合条件②的区间[]；
（2）判断函数
是不是闭函数？若是请找出区间[]；若不是请说明理由；
（3）若
是闭函数，求实数
的取值范围.
（注：本题求解中涉及的函数单调性不用证明，直接指出是增还是减函数即可）
（满分14分）设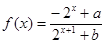
（
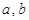为实常数）。
（1）当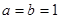
时，证明：①
不是奇函数；
②
是
上的单调递减函数。
（2）设是奇函数，求
与
的值。
（满分14分）已知
是定义在
上的偶函数，当
时，
（1）求
的值；
（2）求
的解析式；并画出简图；
（3）利用图象讨论方程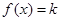
的根的情况。（只需写出结果，不要解答过程）.
（满分14分）某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：
（其中
是仪器的月产量）．
（1）将利润表示为月产量的函数
；
（2）当月产量为何值时，公司所获利润最大？最大利润为多少元？（利润=总收益-总成本）
（满分12分）已知
，
（1）求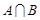
和
；
（2）若记符号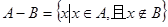
，
①在图中把表示“集合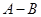
”的部分用阴影涂黑； 
②求
和
.