如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC.
(1)猜想:线段OD与BC有何数量和位置关系,并证明你的结论.
(2)求证:PC是⊙O的切线.
甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比 赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
 |
(1)在图11.1中,“7分”所在扇形的圆心角等于°;将图11.2的统计图补充完整;
(2)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好;
(3)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学 校中的一所挑选参赛选手,请你分析,应选哪所学校?
校中的一所挑选参赛选手,请你分析,应选哪所学校?
如图10,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.
(1)求点C的坐标及直线l2所对应 的函数关系式;
的函数关系式;
(2)求△ABC的面积;
(3)在直线l2上存在一点P,使得PB=PC,请直接写出点P的坐标.
如图9,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD.
(1)用尺规作图的方法,过D点作DF⊥BE,垂足是F(不写作法,保留作图痕迹);
(2)求证:BF=EF.
某市今年计划修建一段全长1500米的景观路,为了尽量减少施工对城市交通的影响,实际施工时,每天的工效比原计划增加20%,结果提前2天完成这一任务,求原计划每天修路多少米?
计算(第(1)小题3分,第(2)小题6分,共9分)
(1)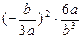 ;(2)
;(2)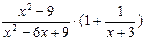 .
.