如图所示,若△ABC为等腰三角形,△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB·CE.
(1)求证:△ADB∽△EAC;
(2)若∠BAC=40°,求∠DAE的度数.
(本小题满分14分)在△ABC中,角A,B,C的对边分别为a,b,c,且
(1)求cosB的值;
(2)若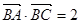 ,且
,且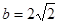 ,求
,求 的值.
的值.
(本小题满分12分)已知向量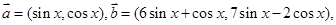
设函数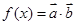
(I)求函数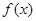 的最大值及此时x的集合;
的最大值及此时x的集合;
(Ⅱ)在A为锐角的三角形ABC中,角A、B、C的对边分别为a、b、c, 且
且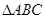
的面积为3, 求a的值。
求a的值。
(本小题满分12分)已知数列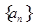 的前
的前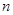 项和为
项和为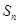 ,且
,且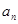 是
是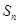 与2的等差中项,数列
与2的等差中项,数列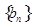 中,
中,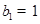 ,点
,点 在直线
在直线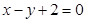 上.
上.
⑴求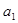 和
和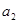 的值;
的值;
⑵求数列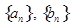 的通项
的通项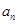 和
和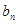 ;
;
⑶ 设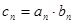 ,求数列
,求数列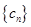 的前n项和
的前n项和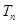 .
.
(本小题满分12分)一缉私艇发现在北偏东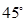 方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东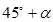 的方向去追,.求追及所需的时间和
的方向去追,.求追及所需的时间和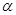 角的正弦值.
角的正弦值.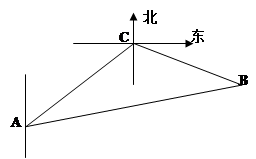
(本小题满分12分)已知二次函数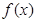 的二次项系数为
的二次项系数为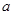 ,且不等式
,且不等式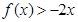 的解集为(1,3)。
的解集为(1,3)。
(1)若方程 有两个相等的实数根,求
有两个相等的实数根,求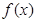 的解析式;
的解析式;
(2)若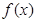 的最大值为正数,求
的最大值为正数,求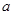 的取值范围。
的取值范围。