如图，已知抛物线与x轴交于A（－1，0）、E（3，0）两点，与y轴交于点B（0，3）。
（1）求抛物线的解析式；
（2）设抛物线顶点为D，求四边形AEDB的面积；
（3）△AOB与△DBE是否相似？如果相似，请给以证明；如果不相似，请说明理由。
已知：如图，在Rt△ABC中，∠C=90°，∠ABC=60°，AC=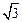
，D为CB延长线上一点，且BD=2AB．求AD的长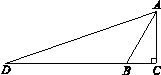
若关于x的方程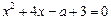 
有实数根．
（1）求a的取值范围；
（2）若a为符合条件的最小整数，求此时方程的根
计算：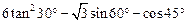
如图，已知抛物线与
轴交于点
，
，与
轴交于点
．
（1）求抛物线的解析式及其顶点
的坐标；
（2）设直线
交轴于点
．在线段
的垂直平分线上是否存在点
，使得点到直线的距离等于点到原点
的距离？如果存在，求出点的坐标；如果不存在，请说明理由；
（3）过点
作轴的垂线，交直线于点
，将抛物线沿其对称轴平移，使抛物线与线段
总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？
已知一个直角三角形纸片
，其中
．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边
交于点
，与边
交于点
．
（1）若折叠后使点
与点
重合，求点的坐标；
（2）若折叠后点落在边
上的点为
，设
，
，试写出
关于
的函数解析式，并确定的取值范围；
（3）若折叠后点落在边上的点为，且使
，求此时点的坐标．