已知函数f(x)=2sin xcos x+cos 2x(x∈R).
(1)当x取什么值时,函数f(x)取得最大值,并求其最大值;
(2)若θ为锐角,且f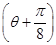 =
=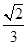 ,求tan θ的值.
,求tan θ的值.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45,点E、F分别为棱AB、PD的中点.
(1)求证:AF∥平面PCE;
(2)求三棱锥C-BEP的体积.
已知数列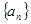 的前
的前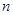 项和
项和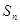 满足
满足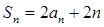
(1)写出数列的前3项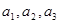 ;
;
(2)求数列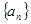 的通项公式.
的通项公式.
在 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 ,
,
(1)求证: ;
;
(2)若 ,求
,求 的值.
的值.
设函数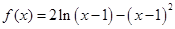 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若关于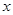 的方程
的方程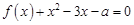 在区间
在区间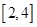 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数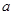 的取值范围.
的取值范围.
已知椭圆 的一个焦点
的一个焦点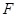 与抛物线
与抛物线 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为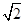 ,倾斜角为
,倾斜角为 的直线
的直线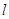 过点
过点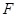 .
.
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为 ,问抛物线
,问抛物线 上是否存在一点
上是否存在一点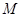 ,使得
,使得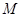 与
与 关于直线
关于直线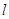 对称,若存在,求出点
对称,若存在,求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.