已知椭圆 的一个焦点
的一个焦点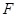 与抛物线
与抛物线 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为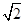 ,倾斜角为
,倾斜角为 的直线
的直线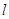 过点
过点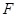 .
.
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为 ,问抛物线
,问抛物线 上是否存在一点
上是否存在一点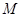 ,使得
,使得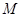 与
与 关于直线
关于直线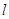 对称,若存在,求出点
对称,若存在,求出点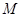 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(本题满分13分)已知点F(1,0),圆E: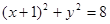 ,点P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.
,点P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.
(1)求动点Q的轨迹Γ的方程;
(2)若直线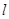 与圆O:
与圆O: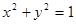 相切,并与(1)中轨迹Γ交于不同的两点A、B.当
相切,并与(1)中轨迹Γ交于不同的两点A、B.当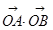 =
=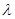 ,且满足
,且满足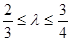 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
(本题满分12分)已知函数f(x)= (
(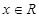 ).
).
(1)求函数f(x)的周期和递增区间;
(2)若函数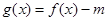 在[0,
在[0,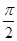 ]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
(本题满分12分)如图所示,在正方体ABCD—A1B1C1D1中,E是棱DD1的中点.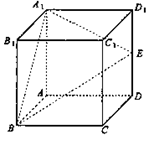
(1)求直线BE和平面ABB1A1所成角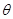 的正弦值;
的正弦值;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
(本题满分12分)某种有奖销售的小食品,袋内印有“免费赠送一袋”或“谢谢品尝”字样,购买一袋若其袋内印有“免费赠送一袋”字样即为中奖,中奖概率为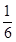 .甲、乙、丙三位同学每人购买了一袋该食品。
.甲、乙、丙三位同学每人购买了一袋该食品。
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数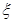 的分布列及数学期望
的分布列及数学期望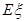 .
.
(本题满分12分)在数列{an}中,已知a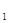 =-20,a
=-20,a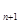 =a
=a +4(n∈
+4(n∈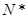 ).
).
(1)求数列{an}的通项公式和前n项和An;
(2)若 (n∈
(n∈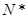 ),求数列{bn}的前n项Sn.
),求数列{bn}的前n项Sn.