(本题满分12分)如图所示,在正方体ABCD—A1B1C1D1中,E是棱DD1的中点.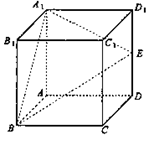
(1)求直线BE和平面ABB1A1所成角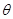 的正弦值;
的正弦值;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
如图,在直三棱柱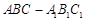 中,
中,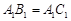 ,
,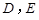 分别是棱
分别是棱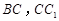 上的点(点
上的点(点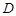 不同于点
不同于点 ),且
),且 为
为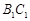 的中点.
的中点.
求证:(1)平面 平面
平面 ;
;
(2)直线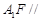 平面
平面 .
.
设函数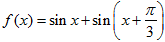 .
.
(1)求f(x)的最小值,并求使f(x)取得最小值的x的集合;
(2)在△ABC中,设角A,B的对边分别为a,b,若B=2A,且 ,求角C的大小.
,求角C的大小.
已知p:方程2x2-2mx+1=0有两个不相等的负实根;q:存在x∈R,
x2+mx+1<0.若p或q为真,p且q为假,求实数m的取值范围.
某网站针对2015年中国好声音歌手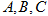 三人进行网上投票,结果如下
三人进行网上投票,结果如下
| 观众年龄 |
支持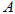 |
支持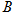 |
支持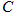 |
| 20岁以下 |
200 |
400 |
800 |
| 20岁以上(含20岁) |
100 |
100 |
400 |
(1)在所有参与该活动的人中,用分层抽样的方法抽取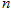 人,其中有6人支持
人,其中有6人支持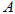 ,求
,求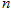 的值.
的值.
(2)在支持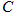 的人中,用分层抽样的方法抽取6人作为一个总体,从这6人中任意选取2人,求恰有1
的人中,用分层抽样的方法抽取6人作为一个总体,从这6人中任意选取2人,求恰有1
人在20岁以下的概率.
设函数fn(x)=xn+bx+c(n∈N+,b,c∈R).
(1)设n≥2,b=1,c=-1,证明:fn(x)在区间 内存在唯一零点;
内存在唯一零点;
(2)设n=2,若对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,求b的取值范围;
(3)在(1)的条件下,设xn是fn(x)在 内的零点,判断数列x2,x3,…,xn,…的增减性.
内的零点,判断数列x2,x3,…,xn,…的增减性.