设函数fn(x)=xn+bx+c(n∈N+,b,c∈R).
(1)设n≥2,b=1,c=-1,证明:fn(x)在区间 内存在唯一零点;
内存在唯一零点;
(2)设n=2,若对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,求b的取值范围;
(3)在(1)的条件下,设xn是fn(x)在 内的零点,判断数列x2,x3,…,xn,…的增减性.
内的零点,判断数列x2,x3,…,xn,…的增减性.
某海边旅游景点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆。为了便于结算,每辆自行车的日租金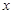 (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用 (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(Ⅰ)求函数 的解析式及其定义域;
的解析式及其定义域;
(Ⅱ)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
阅读下面材料:
根据两角和与差的正弦公式,有 ------①
------① ------②
------②
由①+② 得 ------③
------③
令 有
有
代入③得  .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明: ;
;
(Ⅱ)若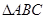 的三个内角
的三个内角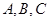 满足
满足 ,试判断
,试判断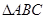 的形状.
的形状.
函数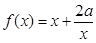
(Ⅰ)判断并证明函数的奇偶性;
(Ⅱ)若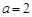 ,证明函数
,证明函数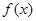 在
在 上单调递增;
上单调递增;
(Ⅲ)在满足(Ⅱ)的条件下,解不等式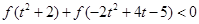 .
.
已知函数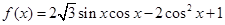
(Ⅰ)求函数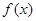 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ)在 中,若
中,若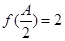 ,
,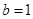 ,
, ,求
,求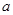 的值.
的值.
设全集 ,已知集合
,已知集合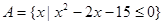 ,集合
,集合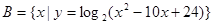 ,.
,.
(Ⅰ)求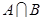 ,
, ;
;
(Ⅱ)记集合 ,集合
,集合 ,若
,若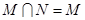 ,求实数
,求实数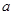 的取值范围.
的取值范围.