在直角梯形 中,
中, ,
,
 ,
, ,如图,把
,如图,把 沿
沿 翻折,使得平面
翻折,使得平面 平面
平面 .
.


(1)求证: ;
;
(2)若点 为线段
为线段 中点,求点
中点,求点 到平面
到平面 的距离;
的距离;
(3)在线段 上是否存在点
上是否存在点 ,使得
,使得 与平面
与平面 所成角为
所成角为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
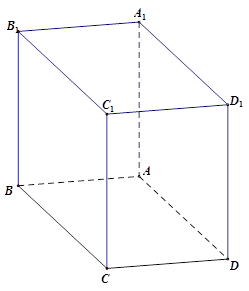
如图:已知四棱柱 的底面是菱形,该菱形的边长为1,
的底面是菱形,该菱形的边长为1,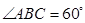 ,
, .
.
(1)设棱形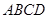 的对角线的交点为
的对角线的交点为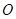 ,求证:
,求证: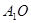 //平面
//平面 ;
;
(2)若四棱柱的体积 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知函数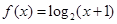 ,当点
,当点 在函数
在函数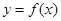 的图象上运动时,点
的图象上运动时,点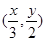 在函数
在函数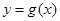 (
(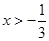 )的图象上运动.
)的图象上运动.
(1)求函数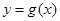 的解析式;
的解析式;
(2)求函数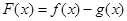 的零点.
的零点.
(3)函数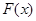 在
在 上是否有最大值、最小值;若有,求出最大值、最小值;若没有请说明理由.
上是否有最大值、最小值;若有,求出最大值、最小值;若没有请说明理由.
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
 |
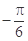 |
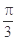 |
 |
 |
 |
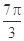 |
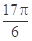 |
 |
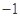 |
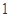 |
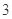 |
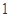 |
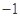 |
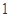 |
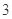 |
(1)根据表格提供的数据求函数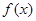 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数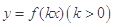 周期为
周期为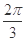 ,当
,当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数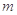 的取值范围.
的取值范围.
(1)当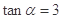 ,求
,求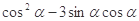 的值;
的值;
(2)设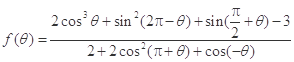 ,求
,求 的值.
的值.
已知函数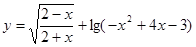 的定义域为
的定义域为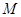 ,
,
(1)求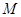 ;
;
(2)当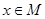 时,求函数
时,求函数 的最小值.
的最小值.