设U=R,集合A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0},若( A)∩B=⌀,求m的值.
A)∩B=⌀,求m的值.
(本小题满分10分)
在△ 中,角
中,角 所对应的边分别为
所对应的边分别为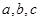 ,已知
,已知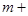

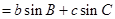
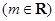 ,且
,且 .
.
(Ⅰ)当 ,且△
,且△ 的面积
的面积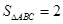 时,求边
时,求边 的值;
的值;
(Ⅱ)当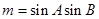 时,求角
时,求角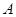 的值.
的值.
(本小题满分14分)
设抛物线 :
:
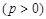 的焦点为
的焦点为 ,过
,过 且斜率为
且斜率为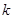 的直线
的直线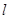 交抛物线
交抛物线 于
于 ,
, 两点,且
两点,且 .
.
(Ⅰ)求抛物线 的标准方程;
的标准方程;
(Ⅱ)已知点 ,且
,且 的面积为
的面积为 ,求
,求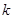 的值.
的值.
设数列 满足
满足 .
.
(Ⅰ)求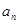 ;
;
(Ⅱ)设 ,
, ,求证:数列
,求证:数列 中
中 最小.
最小.
(本小题满分15分)
对于函数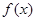 ,若存在
,若存在 ,使
,使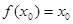 成立,则称
成立,则称 为
为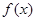 的一个不动点.
的一个不动点.
设函数 (
( ).
).
(Ⅰ)当 ,
,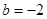 时,求
时,求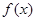 的不动点;
的不动点;
(Ⅱ)设函数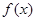 的对称轴为直线
的对称轴为直线 ,
, 为
为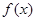 的不动点,当
的不动点,当 时,求证:
时,求证: .
.
(本小题满分15分)
已知椭圆 :
: .
.
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)设直线 与椭圆
与椭圆 交于不同两点
交于不同两点 ,若点
,若点 满足
满足 ,求实数
,求实数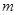 的值.
的值.