如图X15－3所示，已知圆C1：x2＋(y－1)2＝4和抛物线C2：y＝x2－1，过坐标原点O的直线与C2相交于点A，B，定点M的坐标为(0，－1)，直线MA，MB分别与C1相交于点D，E.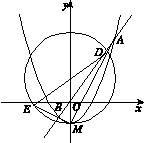
(1)求证：MA⊥MB；
(2)记△MAB，△MDE的面积分别为S1，S2，若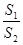
＝λ，求λ的取值范围．
已知函数f(x)=|3x-6|-|x-4|.
(1)作出函数y=f(x)的图象;
(2)解不等式|3x-6|-|x-4|>2x.
已知函数f(x)=|x-1|+|x+3|.
(1)求x的取值范围,使f(x)为常数函数.
(2)若关于x的不等式f(x)-a≤0有解,求实数a的取值范围.
设函数f(x)=|2x-1|+|2x-3|,x∈R.
(1)求关于x的不等式f(x)≤5的解集.
(2)若g(x)=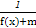
的定义域为R,求实数m的取值范围.
设函数f(x)=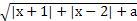
.
(1)当a=-5时,求函数f(x)的定义域.
(2)若函数f(x)的定义域为R,试求a的取值范围.
设f(x)=
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.