如图,在平面直角坐标系xOy中,一次函数y=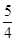 x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.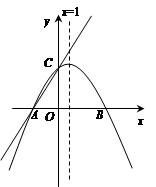
(1)求m的值及抛物线的函数表达式;
(2)若P是抛物线对称轴上一动点,△ACP周长最小时,求出P的坐标;
(3)是否存在抛物在线一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若不存在,请说明理由;
(4)在(2)的条件下过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问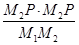 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
生活中很多矿泉水没有喝完便被扔掉,造成极大的浪费,为此数学兴趣小组的同学对某单位的某次会议所用矿泉水的浪费情况进行调查,为期半天的会议中,每人发一瓶500ml的矿泉水,会后对所发矿泉水喝的情况进行统计,大至可分为四种:A:全部喝完;B:喝剩约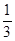 ;C:喝剩约一半;D:开瓶但基本未喝.同学们根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:
;C:喝剩约一半;D:开瓶但基本未喝.同学们根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题: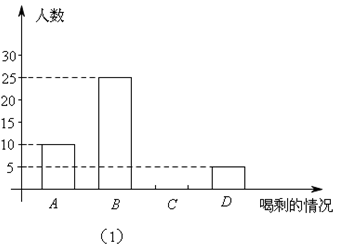
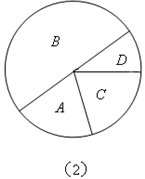
(1)参加这次会议的有多少人?在图(2)中D所在扇形的圆心角是多少度?并补全条形统计图;(计算结果请保留整数).
(2)若开瓶但基本未喝算全部浪费,试计算这次会议平均每人浪费的矿泉水约多少毫升?
(3)据不完全统计,该单位每年约有此类会议60次,每次会议人数约在40至60人之间,请用(2)中计算的结果,估计该单位一年中因此类会议浪费的矿泉水(500ml/瓶)约有多少瓶?(可使用科学计算器)
如图,在平面直角坐标系中,反比例函数 (x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6) .
(x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6) .
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
甲、乙、丙3人聚会,每人带了一件从外盒包装上看完全相同的礼物(里面的东西只有颜色不同),将3件礼物放在一起,每人从中随机抽取一件.
(1)下列事件是必然事件的是().
A.乙抽到一件礼物
B.乙恰好抽到自己带来的礼物
C.乙没有抽到自己带来的礼物
D.只有乙抽到自己带来的礼物
(2)甲、乙、丙3人抽到的都不是自己带来的礼物(记为事件A),请列出事件A的所有可能的结果,并求事件A的概率.
先化简,再求值: ,在0,1,2,三个数中选一个合适的,代入求值.
,在0,1,2,三个数中选一个合适的,代入求值.
如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
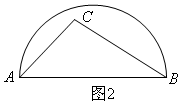
(1)在图1中,画出△ABC的三条高的交点;
(2)在图2中,画出△ABC中AB边上的高.