已知矩阵
 ,若矩阵
,若矩阵 属于特征值6的一个特征向量为
属于特征值6的一个特征向量为 ,属于特征值1的一个特征向量
,属于特征值1的一个特征向量 .
.
(1)求矩阵 的逆矩阵;
的逆矩阵;
(2)计算
(本小题满分13分)
如图,已知正方形ABCD和梯形ACEF所在的平面互相垂直, ,CE//AF,
,CE//AF,
(I)求证:CM//平面BDF;
(II)求异面直线CM与FD所成角的大小;
(III)求二面角A—DF—B的大小。
(本小题满分13分)
已知点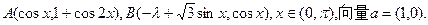
(I)若向量 的值;(II)若向量
的值;(II)若向量 的取值范围。
的取值范围。
(本小题满分12分)已知函数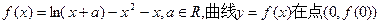 处的切线恰好为
处的切线恰好为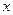 轴。(I)求
轴。(I)求 的值;(II)若区间
的值;(II)若区间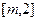 恒为函数
恒为函数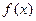 的一个单调区间,求实数
的一个单调区间,求实数 的最小值;(III)记
的最小值;(III)记 (其中
(其中 ),
), 的导函数,则函数
的导函数,则函数 是否存在极值点?若存在,请找出极值点并论证是极大值点还是极小值点;若不存在,请说明理由。
是否存在极值点?若存在,请找出极值点并论证是极大值点还是极小值点;若不存在,请说明理由。
对于正整数
,用
表示关于
的一元二次方程
有实数根的有序数组
的组数,其中
(
和
可以相等);对于随机选取的
(
和
可以相等),记
为关于
的一元二次方程
有实数根的概率.
(1)求
和
;
(2)求证:对任意正整数
,有
。
A.选修4 - 1:几何证明选讲
如图,在四边形
中,
.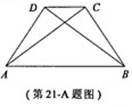
求证:
.
B.选修4 - 2:矩阵与变换
求矩阵
的逆矩阵.
C.选修4 - 4:坐标系与参数方程
已知曲线
的参数方程为
(
为参数,
),求曲线
的普通方程.
D.选修4 - 5:不等式选讲
设
,求证:
.