已知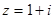 ;
;
(1)如果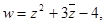 求
求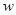 的值;
的值;
(2)如果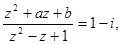 求实数
求实数 的值.
的值.
我国是水资源比较贫乏的国家之一.目前,某市就节水问题,召开了市民听证
会,并对水价进行激烈讨论,会后拟定方案如下:以户为单位,按月收缴,水价按照每户每
月用水量分三级管理,第一级为每月用水量不超过12吨,每吨3.5元;第二级计量范围为
超过12吨不超过18吨部分,第三级计量范围为超出18吨的部分,一、二、三级水价的单
价按1:3:5计价.
(1)请写出每月水费 (
( 元)与用水量
元)与用水量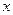 (吨)之间的函数关系;
(吨)之间的函数关系;
(2)某户居民当月交纳水费为63元,该户当月用水多少吨?
已知函数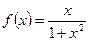 .
.
(1)证明函数具有奇偶性;
(2)证明函数在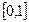 上是单调函数;
上是单调函数;
(3)求函数在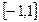 上的最值.
上的最值.
已知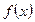 是二次函数,满足
是二次函数,满足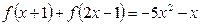 ,
, 求函数
求函数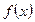 的
的
解析式、值域,并写出函数的单调递减区间.
已知集合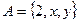 ,
,
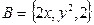 ,若
,若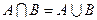 ,求实数
,求实数 、
、 的
的
值 .
.
集合 ,
,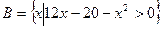 ,求
,求 ,
,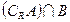 ,
, .
.