定义F(x,y)=(1+x)y,x,y∈(0,+∞).令函数f(x)=F(1,log2(x2-4x+9))的图象为曲线C1,曲线C1与y轴交于点A(0,m),过坐标原点O向曲线C1作切线,切点为B(n,t)(n>0),设曲线C1在点A,B之间的曲线段与线段OA,OB所围成图形的面积为S,求S的值.
如图，△ABC的角平分线AD的延长线交它的外接圆于点E.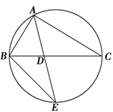
(1)证明：△ABE∽△ADC；
(2)若△ABC的面积S＝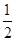
AD·AE，求∠BAC的大小．
已知函数f(x)＝sin 
＋cos
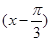，g(x)＝2sin2
.
(1)若α是第一象限角，且f(α)＝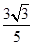
.求g(α)的值；
(2)求使f(x)≥g(x)成立的x的取值集合．
已知函数f(x)＝2sin ωx·cos ωx＋2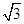
cos2ωx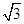－(其中ω>0)，且函数f(x)的周期为π.
(1)求ω的值；
(2)将函数y＝f(x)的图象向右平移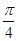
个单位长度，再将所得图象各点的横坐标缩小到原来的
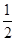倍(纵坐标不变)得到函数y＝g(x)的图象，求函数g(x)在
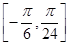上的单调区间．
已知函数f(x)＝Asin(ωx＋φ)(A>0，ω>0，|φ|< 
)的图象的一部分如图所示．
(1)求函数f(x)的解析式；
(2)当x∈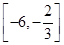
时，求函数y＝f(x)＋f(x＋2)的最大值与最小值及相应的x的值．
已知函数f(x)＝ex－ln(x＋m)．
(1)设x＝0是f(x)的极值点，求m，并讨论f(x)的单调性；
(2)当m≤2时，证明f(x)>0.