已知函数f(x)＝2sin ωx·cos ωx＋2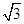
cos2ωx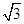－(其中ω>0)，且函数f(x)的周期为π.
(1)求ω的值；
(2)将函数y＝f(x)的图象向右平移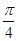
个单位长度，再将所得图象各点的横坐标缩小到原来的
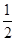倍(纵坐标不变)得到函数y＝g(x)的图象，求函数g(x)在
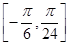上的单调区间．
设椭圆C1的方程为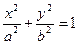
(a＞b＞0)，曲线C2的方程为y=
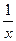，且曲线C1与C2在第一象限内只有一个公共点P.
（1）试用a表示点P的坐标；
（2）设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；
（3）记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个. 设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试求函数f(a)=min{g(a), S(a)}的表达式.
把一个长、宽、高分别为25 cm、20 cm、5 cm的长方体木盒从一个正方形窗口穿过，那么正方形窗口的边长至少应为多少？
已知A（1，1）为椭圆
=1内一点，F1为椭圆左焦点，P为椭圆上一动点
求｜PF1｜+｜PA｜的最大值和最小值.
设A={(x,y)｜y=
,a＞0}，B={(x,y)｜(x–1)2+(y–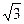
)2=a2,a＞0},且A∩B≠
，求a的最大值与最小值.
设关于x的方程sinx+
cosx+a=0在（0,π）内有相异解α、β.
（1）求a的取值范围；
（2）求tan(α+β)的值.